Расчет основных параметров ветротепловой установки (Глава 2 магистерской работы), страница 13

если ограничится умеренным значением угла атаки, то можно заменить

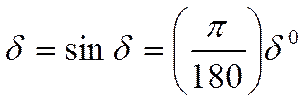,отсюда   

.

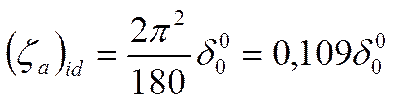С увеличением относительной толщины d/L и с увеличением   смещения назад fx/L максимальной стрелы прогиба, несколько снижается угол наклона кривой подъемной силы. В этом же направле­нии влияет и вязкость, потому что поток отклоняется от танген­циального обтекания хвостовой части профиля. Согласно большому числу экспериментальных данных можно счи­тать

ζ_а = (0,092 до 0,1)δ₀⁰          

и соответственно 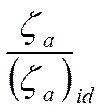= 0,85 ÷ 0,92 ≡η, который растет с уменьшением d/L и f/L. Таким   образом,   можно   считать          ζ_а  =2∙π ∙n∙ sin∙δ₀

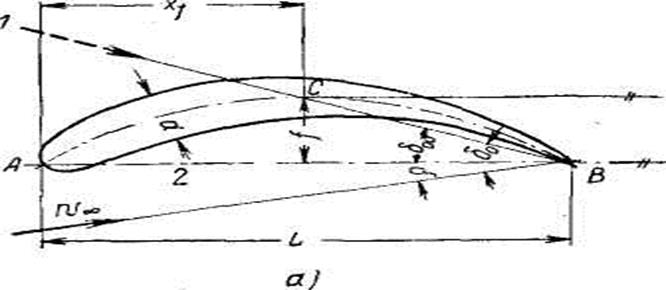
Этим объясняется параллельное расположение линий ζ_a, δ на       рис. 2.9. Между углом атаки δ, измеренным для любого исходного напра­вления, и углом δ₀, отнесенным к направлению нулевой подъем­ной силы, существует зависимость (см. рис. 3.0, а)

δ₀ — δ = δ_oo_

где δ₀₀ означает угол между направлением СВструи без подъемной силы и выбранным исходным направлением АВ (не принимая во вни­мание изменения знака δ₀). Если известно это нулевое направле­ние δ₀₀, то коэффициент подъемной силы определяется выражением:

                               ζ_a=k(δ⁰-δ⁰₀₀)

                                                   б)

Рис. 3.0. Направление нулевой подъемной силы и хорды любого профиля:  1)-направление потока, соответствующее ζ_a = 0;     2)-хорда профиля.

при k= 0,092 ÷ 0,10, с возрастанием этой величины при снижении значения d/L и fx/L,  с уменьшением шероховатости  поверхности и увеличением числа Рейнольдса.

Большое количество формул можно свести к одной с достаточно точным определением подъемной силы для любого профиля, если известно направление нулевой подъемной силы. В особенности это существенно потому, что позволяет при­менять особенно благоприятные ламинарные профили в сочетании с подходящей скелетной линией. Для облегчения последнего мы выберем исходным направлением для отсчета углов атаки S не раз­личные направления, указанные на рис. 3.0, а соединительную линию АВ конечных точек скелетных линий, так называемую хорду профиля (рис. 3.0), как это в настоящее время все больше приме­няется на практике. Она не слишком отличается от исходного направления, указанного на рис. 3.0, так что допустима простая их замена в пределах достижимой точности. Для большого коли­чества профилей они даже полностью совпадают.

Определение направления нулевой подъемной силы δ₀₀ изолиро­ванного профиля точно решено для идеальной жидкости и бесконечно тонкого профиля в виде дуги круга (см. рис. 3.0, б), когда соедини­тельная прямая между наивысшей точкой С и точкой вытекания В соответствует направлению потока, не создающего подъемной силы. В первом приближении, по-видимому, можно допустить, что это решение можно применить также для любой другой формы тонкого профиля (например, в виде параболы) и даже на скелетную линию толстого профиля, причем тогда С означает точку касания каса­тельной, параллельной к хорде профиля АВ. Но при этом не учи­тывается, очевидно, влияние вязкости и изменение толщины. Эти факторы можно оценить только на основании опыта. Согласно много­численным измерениям профилей различных толщины и кривизны, приведенным в отчете    № 824 NACA, можно вывести следующую эмпирическую зависимость:

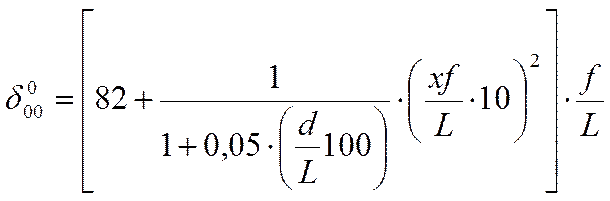
При этом (согласно рис. 3.0) означает: 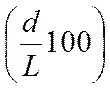 — максимальную толщину в процентах от длины хорды L;

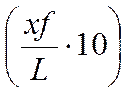— расстояние наибольшей стрелы прогиба скелетной линии от передней кромки профиля в десятых долях хорды L(смещение назад кривизны);

 - отношение  наибольшей стрелы  прогиба скелетной линии к       хорде L.

Следует учесть, что 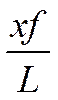 -не представляет теперь смещения  назад наибольшей толщины, а смещение максимальной кривизны, кото­рое, например, при применении дуги круга в качестве скелетной линии всегда равняется 0,5, так что 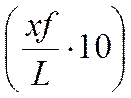= 5. Другие смеще­ния максимальной кривизны, очевидно могут быть получены с помощью параболической скелетной линии. Вообще говоря коэффициенты сопротивления ζ_ω профилей с любой скелетной линией и с любым распределением толщины (аналогично, как у ранее рассмотренных профилей, создаваемых путем утолщения или утонения) неизвестны.