Практическая работа № 1 «Рассмотрение классических примеров теории вероятностей»

Практическая работа №1

Задача 1.

            Пусть в некоторой комнате присутствует r человек, и мы держим пари, что из этих r человек по крайней мере двое родились в один и тот же день, т.е. в один и тот же месяц и одного итого же числа. Мы хотим определить значение r, для которого пари будет честным.

            Решение. Немногие бы согласились заключить это пари на равных условиях, если число людей в комнате меньше 100. Большинство назвало бы в качестве приемливого количества людей 150. Однако мы увидим, что при r = 150 имеется примерно 45×10 шансов против одного, что по крайней  мере у двоих присутствующих день рождения один и тот же. Мы увидим также, что пари следует держать на равных условиях уже при наличии 23 человек в комнате.

            Найдем сначала вероятность того, что никакие два из r человек не имеют одного итого же дня рождения. Для дня рождения каждого человека имеется 365 возможностей. Тогда для дней рождения r человек имеется 365возможностей. Для нахождения вероятности того, что никакие двое из присутствующих не имеют одного итого же дня

Число человек    в комнате	Вероятность совпадения дней рождения по край- ней мере двух человек	Приблизительное условие          честного пари
5          10          15          20          21          22          23          24          25          30          40          50          60          70          80          90        100        125        150	0,027                0,117                0,253                0,411                0,444                0,476                0,507                0,538                0,569                0,706                0,891                0,970                0,994	70 : 100               80 : 100               91 : 100             103 : 100             103 : 100             132 : 100             242 : 100             819 : 100               33 : 1             169 : 1           1200 : 1         12000 : 1        160000 : 1      33 × 10 : 1      31 × 10 : 1     45 × 10 : 1

рождения, мы должны найти число тех возможностей для дней рождения, в которых никакой день не фигурирует дважды. Первый человек может иметь в качестве своего дня рождения любой из 365 дней. Каждый из них оставляет для второго человека (день рождения которого должен быть другим !) 364 возможности. Для третьего человека имеется 363 возможности, если требовать чтобы его день рождения был отличен от дней рождения двух предыдущих людей и т.д. Таким образом, вероятность того, что в группе из r человек никакие два человека не имеют одного и того же дня рождения, равна

q=.

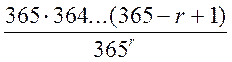
            Вероятность того, что по крайней мере два человека имеют один и тот же день рождения, равна  .

Задача 2.

            Какова вероятность того, что при двух бросаниях монеты оба раза сверху окажется герб?

            Решение. В этом случае опыт состоит в том, что мы два раза подбрасываем монету и оба раза отмечаем, какая сторона монеты оказывается сверху. Этот опыт может привести к следующим трем исходам :  или оба раза сверху окажется герб, или оба раза сверху окажется решетка, или же один раз сверху окажется герб и один раз решетка. Число благоприятных исходов здесь, очевидно, равно 1; поэтому можно было бы подумать, что искомая вероятность равна 1/3. Однако  при первом бросании монеты сверху может оказаться или герб или решетка; оба эти исхода, очевидно, равновероятны в силу симметрии монеты. При втором бросании также сверху может оказаться герб или решетка. Комбинируя два возможных исхода первого бросания с двумя возможными исходами второго бросания, мы получим всего четыре различных исхода, а именно: герб-герб, герб-решетка, решетка-герб, решетка-решетка. Эти четыре исхода будут равновероятны: каждый из них соответствует одному определенному исходу первого бросания и одному определенному исходу второго бросания , а то, о каких именно исходах отдельных бросаний идет речь, конечно, не существенно в силу полной равноправности обеих сторон монеты. Отсюда и следует, что искомая вероятность равна 1/4; ранее получился неверный результат из-за того, что мы не различали, в каком порядке выпадут герб и решетка, и объединили два равновероятных исхода (герб-решетка и решетка-герб) в один, что нарушило равновероятность исходов.

Задача 3.

            В урне содержится 5 белых, 10 красных и 6 черных шаров, различающихся только цветом. Из урны наугад вынимается один шарю Какова вероятность появления белого шара?

            Решение. Здесь элементарным исходом является извлечение из урны любого шара. Число всех таких исходов равно числу шаров в урне, т.е. 21. Интересующее нас событие А состоит в том что из урны вымут белый шар. Очевидно, что число m событий, благоприятствующих появлению события А, равно числу белых шаров в урне, т.е. 5. Таким образом:

p(A) =  .

Задача 4.

            Куб, все грани которого окрашены, распилен на 125 кубиков одинакового размера. Все кубики перемешаны. Определить вероятность того, что кубик, извлеченный на удачу, будет иметь три окрашенные грани.