В урне три синих шара, восемь красных и девять белых. Все шары одного размера и веса. Как велики вероятности выхода синего, красного и белого шара из урны?
Решение. Случаев,
благоприятных выходу синего шара m![]() = 3,
благоприятных выходу красного - m
= 3,
благоприятных выходу красного - m![]() = 8 и благоприятных выходу белого - m
= 8 и благоприятных выходу белого - m![]() = 9.
= 9.
Всех равновозможных случаев n = 20.
P(A) = ![]() = 0,15;
= 0,15;![]() P(B) =
P(B) = ![]() = 0,40; P(C) =
= 0,40; P(C) = ![]() =
0,45.
=
0,45.
Как велика вероятность вскрытия не менее 8 очков при бросании двух игральных костей?
Решение. Число всех равновозможных случаев n = 36.
Благоприятными будут только те случаи, при которых число вскрывшихся очков будет или 8, или 9, или 10, или 11, или 12.
|
Число очков |
8 |
9 |
10 |
11 |
12 |
|
1-я кость |
2 3 4 5 6 |
3 4 5 6 |
4 5 6 |
5 6 |
6 |
|
2-я кость |
6 5 4 3 2 |
6 5 4 3 |
6 5 4 |
6 5 |
6 |
|
Сумма |
8 8 8 8 8 |
9 9 9 9 |
10 10 10 |
11 11 |
12 |
|
m |
5 |
4 |
3 |
2 |
1 |
m =
5+4+3+2+1 = 15; p =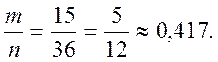
Как велика вероятность, что при бросании трех монет вскрываются два герба?
Решение. Переберем все равновозможные комбинации вскрытия герба и не герба, из которых выделим случаи, благоприятные вскрытию двух гербов из трех возможных.
Г Г Г, Г Г Н, Г Н Г, Г Н Н, Н Н Н, Н Г Г , Н Г Н, Н Н Г.
Благоприятных случаев - 3(подчеркнуты), всех равновозможных - 8.
p = 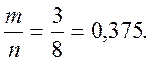
В урне 3 белых шара и 7 черных. Как велика вероятность вынуть два черных шара?
Решение. Число всех равновозможных случаев выбора различных пар шаров равно числу сочетаний из 10 по два:
n = C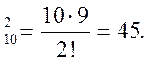
Число благоприятных случаев получим, присоединяя к каждому черному шару любой из остальных,
С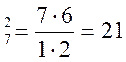 ; p =
; p = 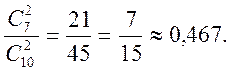
В урне пять шаров: черный №1, черный №2, белый №1, белый №2, белый №3.
А и Б играют на следующих условиях. А вынимает один шар и выигрывает в том случае, если он вынет шар с №1 или черный. Как велика вероятность выигрыша для А?
Решение. Число благоприятных случаев m = 3 (черный №1, черный №2 и белый №1).
p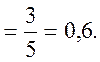
Билеты некоторой лотереи выпускаются ежедневно сериями по 100 билетов, в числе которых имеется 10 выигрышных. Розыгрыш лотереи назначен тогда, когда прекратится покупка билетов, но не позже чем через месяц. Как велика вероятность выигрыша в этой лотерее?
Решение. Число билетов здесь неопределенно: оно не менее 10 и не более 300, но отношение числа выигранных билетов к числу всех выпущенных все время остается вполне определенным числом: 1/10. Следовательно, вероятность выигрыша на один билет
р = 0,1.
Имеется три килограмма калиброванных стальных шаров. Два килограмма шаров окрасили в красный цвет, а один килограмм - в синий цвет. Как велика вероятность вынуть из ящика с этими шарами красный шар?
Решение. Хотя число шаров нам совершенно неизвестно, тем не менее вероятность может быть вычислена на основании ее определения. m - пропорционально двум килограммам, n - пропорционально трем килограммам.
Искомая вероятность
p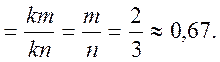
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.