Решение. Всего кубиков n = 125. Извлечение каждого такого кубика является элементарным исходом в данном опыте. Ожидаемому событию А-извлечению кубика с тремя окрашенными гранями - благоприятствует m = 8 исходов (три окрашенные грани имеет только тот кубик, одна из вершин которого совпадает с вершиной куба).
Отсюда
p(A) = ![]() = 0,032.
= 0,032.
Бросаются два интегральных кубика. Какова вероятность того, что сумма очков окажется равной 7?
Решение.
Интегральный кубик может упасть шестью различными способами. Таким образом,
общее число возможных элементарных исходов равно ![]() . Подсчитаем число элементарных исходов
благоприятствующих событию А (сумма очков равна 7). Семь очков получится, если
на первом и втором кубиках будет соответственно: 1 и 6, 2 и 5, 3 и 4, 5 и 2, 6
и 1 очков, т.е. имеется всего 6 исходов, благоприятствующих событию А.
Следовательно, искомая вероятность равна
. Подсчитаем число элементарных исходов
благоприятствующих событию А (сумма очков равна 7). Семь очков получится, если
на первом и втором кубиках будет соответственно: 1 и 6, 2 и 5, 3 и 4, 5 и 2, 6
и 1 очков, т.е. имеется всего 6 исходов, благоприятствующих событию А.
Следовательно, искомая вероятность равна
p(A) = 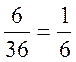 .
.
Слово “керамит” составлено из букв разрезной азбуки. Затем карточки с буквами перемешиваются и из них извлекаются по очереди четыре карточки. Какова вероятность, что эти четыре карточки составят слово “река”?
Решение. Элементарным
исходом является извлечение четырех карточек из семи. По четыре карточки из
семи можно извлечь А![]() способами.
Ожидаемому событию А (выпадение требуемого слова) соответствует только один
исход.
способами.
Ожидаемому событию А (выпадение требуемого слова) соответствует только один
исход.
Таким образом,
p(A) = ![]() =
= ![]() .
.
В партии из 50 деталей 5 нестандартных. Определить вероятность того, что среди выбранных на удачу для проверки шести деталей две окажутся нестандартными.
Решение. Элементарным
исходом является выборка любых шести изделий из пятидесяти. Число n всех таких
исходов, очевидно, равно числу сочетаний из пятидесяти по шесть, т.е. С![]() . Нас интересует событие А, состоящее в
том, что две из шести деталей нестандартные. Благоприятным исходом для А
является любые шесть деталей, из которых две нестандартные и четыре - стандартные.
Такого рода групп по шесть деталей имеется С
. Нас интересует событие А, состоящее в
том, что две из шести деталей нестандартные. Благоприятным исходом для А
является любые шесть деталей, из которых две нестандартные и четыре - стандартные.
Такого рода групп по шесть деталей имеется С![]() × С
× С![]() (так как С
(так как С![]() -число всевозможных пар нестандартных деталей, а С
-число всевозможных пар нестандартных деталей, а С![]() - число всевозможных четверок стандартных деталей и
каждая пара нестандартных деталей может оказаться в одной группе с каждой
четверкой стандартных деталей).
- число всевозможных четверок стандартных деталей и
каждая пара нестандартных деталей может оказаться в одной группе с каждой
четверкой стандартных деталей).
Таким образом,
p(A) = 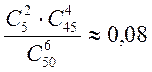 .
.
r элементарных частиц регистрируются R счетчиками, при чем каждая из частиц может с одинаковой вероятностью попасть в любой из счетчиков. Найти вероятность того, что: а) в определенных R счетчиках окажется по одной частице; б) в каких-то R счетчиках окажется по одной частице.
Решение. Здесь элементарным
исходом является размещение r частиц по R счетчикам. Так
как каждая частица имеет R различных возможностей (частица может
попасть в 1-й счетчик, или во 2-й, или в R-й), то число n всех исходов,
т. е. число всех возможных размещений частиц посчетчикам, равно R![]() .
.
В случае а) интересующее нас событие А состоит в том, что в определенных R счетчиках окажется по одной частице. Благоприятным исходом для А является размещение частиц по определенным счетчикам в определенном порядке. Таким образом, число m благоприятствующих размещений равно r!
Откуда
p(A) = ![]() .
.
В случае б) событие А
состоит в том, что в любых R счетчиках окажется по одной частице.
Благоприятным исходом для А в этом случае является размещение частиц по любой
группе из r счетчиков. Так
как таких групп будет С![]() и в каждой
группе возможно размещение r частиц r! способами, то
число m
благоприятствующих размещений равно С
и в каждой
группе возможно размещение r частиц r! способами, то
число m
благоприятствующих размещений равно С![]() ×
×![]() r!
r!
Отсюда
p(A) = 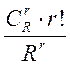 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.