Использование современной компьютерной техники и программного обеспечения для определения зависимости температуры раствора от величины pH раствора, страница 7

Подставляя поочерёдно в уравнение исходные значения  получаем теоретические значения . Затем вычисляем , пользуясь формулой (17):

Затем по формуле (18) вычисляем коэффициент детерминированности:

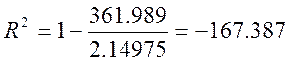- не подходит.

2.  Вычисление коэффициента детерминированности по уравнению для данных, не объединенных в группы.

Подставляя в уравнение исходные значения  получаем теоретические значения . Затем аналогично первому пункту вычисляем , пользуясь формулой (18):

По формуле (17) вычисляем коэффициент детерминированности:

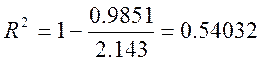
3.  Вычисление коэффициента детерминированности по уравнению, вычисленному методом наименьших квадратов.

Аналогично вычисляем коэффициент детерминированности для уравнения (21):

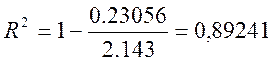
Вычисление коэффициента детерминированности           Таблица 12

 

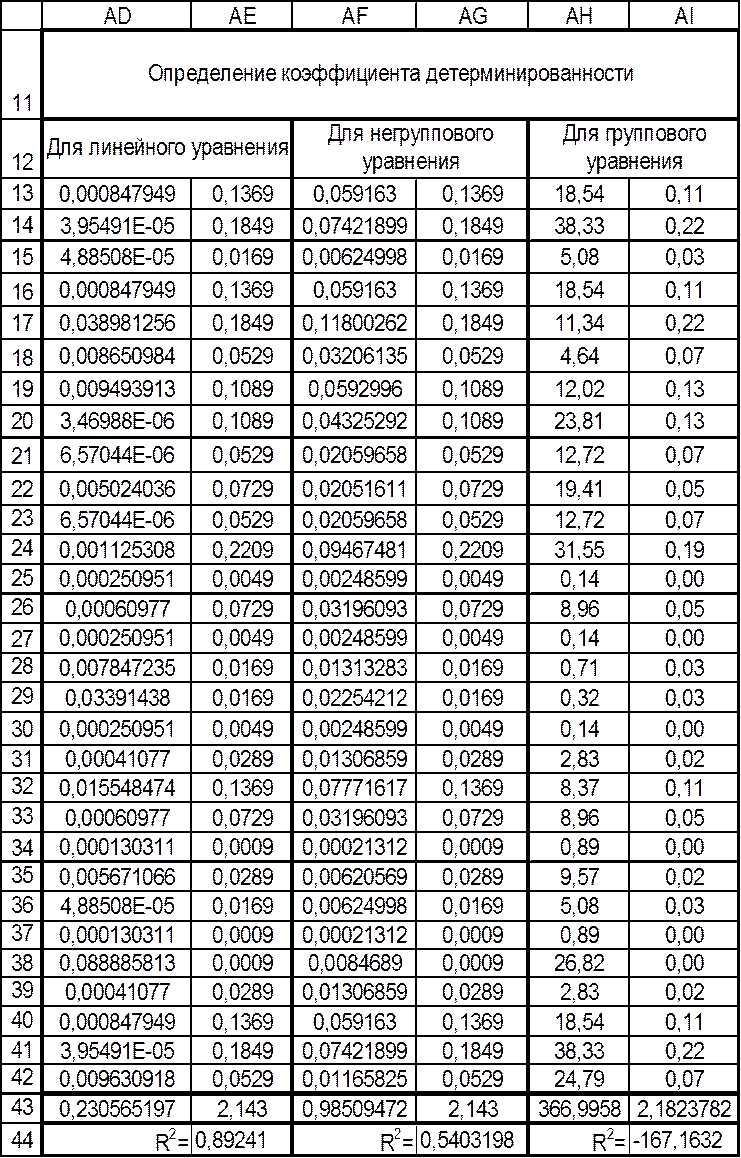
3.4. Обработка полученных результатов.

В результате найдены три уравнения регрессии. Находим для каждого уравнения теоретические значения y подстановкой в найденную формулу значения x. Для этого воспользуемся Excel. Результат вычислений представлен на рисунке 3:

Вид окна Excel c теоретическими значениями Y                Таблица 13

   

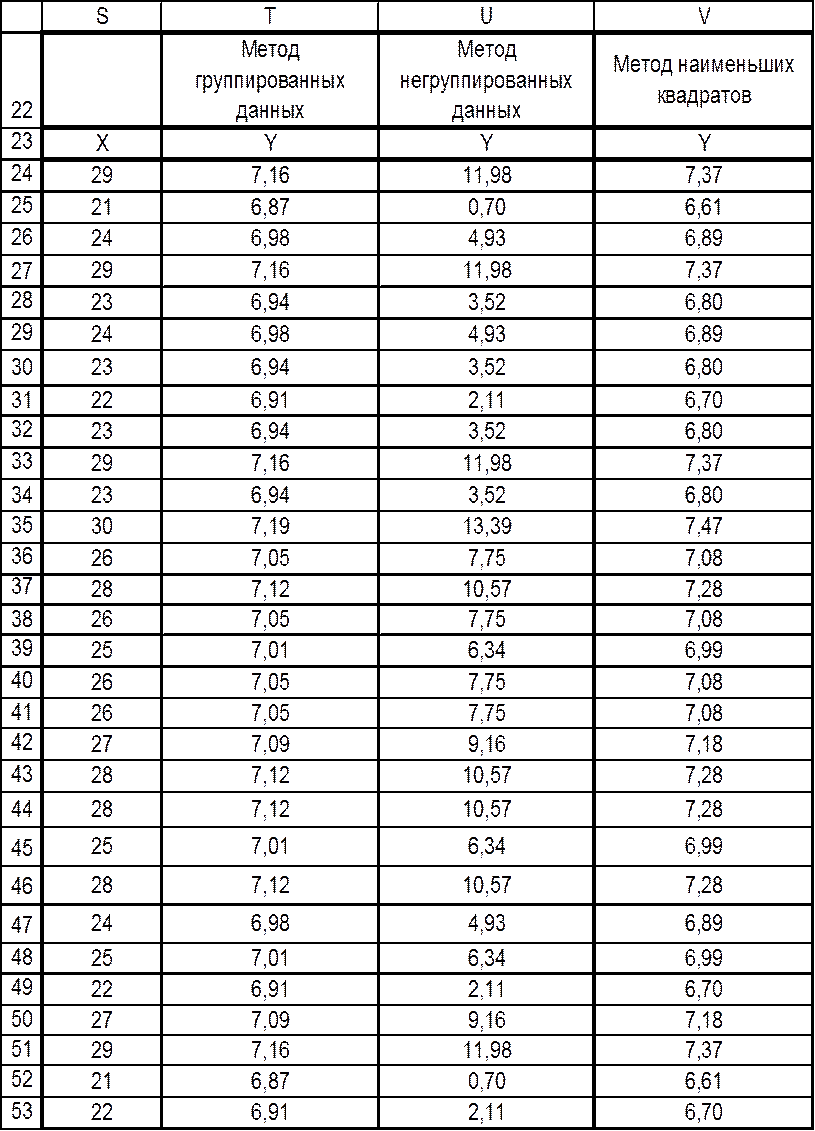
По полученным теоретическим значениям y составим в Excel графики данных уравнений (см. рисунок 2): 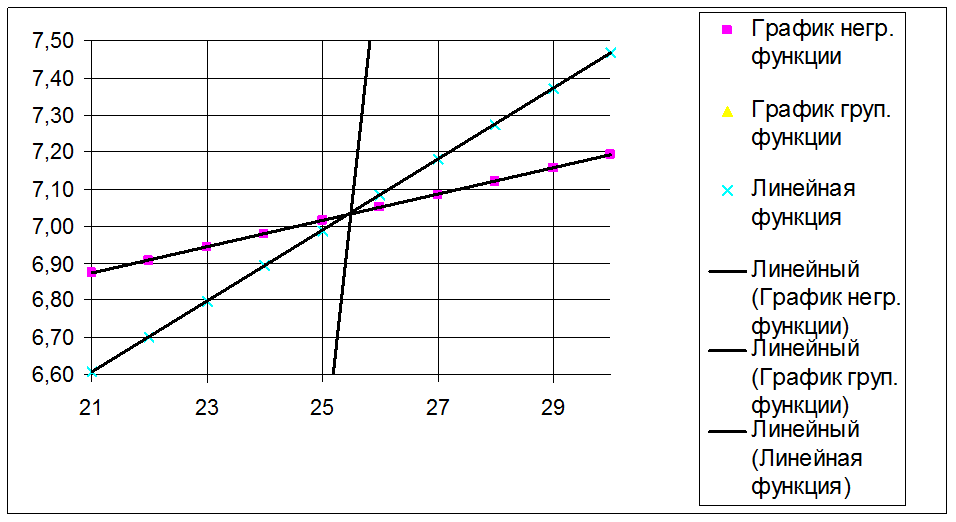Рис.2 Графики теоретических значений Y

4. Разработка алгоритма.

Этот подраздел содержит укрупнённый алгоритм и его описание, а также детали алгоритма.

4.1. Укрупнённый алгоритм и его описание.

Чтобы решить задачу составим программу, которая будет обеспечивать выполнение следующих шагов:

·  Чтение файла input.txt;

• Расчёт корреляционной таблицы;

·  Вычисление уравнения регрессии по группированным данным;

·  Запись таблицы в файл Table.txt;

·  Вычисление уравнения регрессии по негруппированным данным;

·  Вычисление уравнения регрессии методом наименьших квадратов;

·  Запись в Output.txt.

Разделим поставленную задачу на 7 процедур. Первая процедура вводит начальные данные из файла. Вторая процедура вычисляет значения в корреляционной таблице. Третья процедура вычисляет уравнения регрессии по группированным данным. Четвёртая процедура записывает таблицу в файл Table.txt. Пятая процедура  вычисление уравнения регрессии по негруппированным данным. Шестая процедура вычисление уравнения регрессии методом наименьших квадратов. Седьмая процедура запись в Output.txt.

5. Составление программы.

В этот раздел входит описание используемых переменных массивов и констант, файловый ввод данных, пояснение к циклам ветвлениям, соответствие между блок-схемой и программой. Для составления программы используется язык программирования Turbo Pascal 7.0

5.1. Описание используемых переменных, массивов

При написании программы на языке программирования Pascal было использовано достаточно много различных переменных и массивов. Дадим им краткую характеристику.

Road_Input, Road_Output, Road_Table – константы, которые содержат пути к входному, выходному и табличному файлам.

N – константа, содержащая число произведённых измерений.

K – константа, содержащая количество интервалов.

File_Input, File_Output, File_Table – файловые переменные, предназначенные для работы с входными и выходными файлами.

Matrix – массив, содержащий исходные табличные данные.

Matrix_Teor – массив, содержащий теоретические значения функции.

Table – двумерный массив, состоящий из чисел наблюдений, попавших в интервал j по признаку Y и в интервал i по признаку X.

X_Min, X_Max, Y_Min, Y_Max – наибольшие и наименьшие значения X и Y взятые из таблицы исходных данных.

Hx, Hy – интервалы изменения X и Y в пределах их наибольших и наименьших значений.

Sered_intX, Sered_intY – середины интервалов по признакам X и Y соответственно.

Nxi, Nyj – число наблюдений, попавших в интервал i по признаку X и в интервал j по признаку Y соответственно.

UsZnach_YXi , UsZnach_XYj – условные средние значения признака Y для наблюдений, попавших в интервал i по признаку X и признака X для наблюдений, попавших в интервал j по признаку Y.

Sum1, Sum2, Sum3 – переменные, хранящие значения сумм для вычисления коэффициентов корреляции.