Расчёт коэффициента корреляции по группированным данным, выполняется по формуле (7)
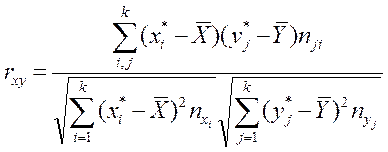 (7)
(7)
где 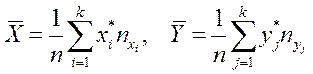 (8)
(8)
Уравнение прямой линии, относительно которой наилучшим образом расположены условные средние значение Y, может быть найдено по формуле (9)
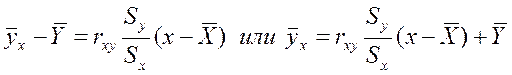 (9)
(9)
При вычислениях по негруппированным данным значение ![]() вычисляется по
формуле (5), значения
вычисляется по
формуле (5), значения ![]() -
по формуле (6), а величины
-
по формуле (6), а величины ![]() - по формуле (10)
- по формуле (10)
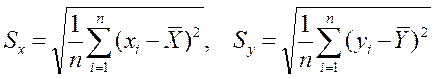 (10)
(10)
При
вычислениях по группированным данным значение ![]() вычисляется по формуле (7),
значения
вычисляется по формуле (7),
значения ![]() -
по формуле (8), а величины
-
по формуле (8), а величины ![]() - по формуле (11)
- по формуле (11)
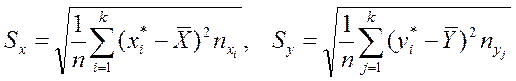 (11)
(11)
Величины, входящие в формулы (10) и (11), определены выше.
В случае двух переменных (X,Y) уравнение линейной регрессии представлено многочленом первой степени
![]() (12)
(12)
Неизвестные параметры ![]() определяются методом наименьших
квадратов, исходя из требования
определяются методом наименьших
квадратов, исходя из требования
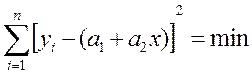 (13)
(13)
Найдя производные уравнения (13) по ![]() и приравняв их нулю, получим
систему нормальных уравнений для определения неизвестных параметров
и приравняв их нулю, получим
систему нормальных уравнений для определения неизвестных параметров ![]() и
и ![]() (14)
(14)
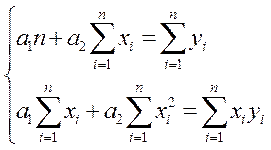 (14)
(14)
Система уравнений (14) может быть решена матричным методом по формуле (15)
![]() (15)
(15)
где матрицы - А, В, Х:
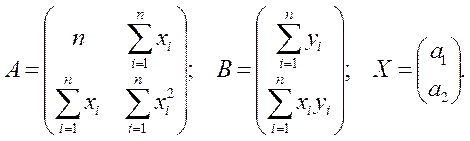 (16)
(16)
2.3 Вычисление коэффициента детерминированности.
Для
количественной оценки соответствия теоретической линии регрессии с
эмпирическими данными используется коэффициент детерминированности ![]() ,
вычисляемый по формуле (17),
,
вычисляемый по формуле (17),
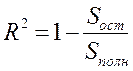 (17)
(17)
где ![]() суммы
квадратов, вычисляемые соответственно по формулам (18),
суммы
квадратов, вычисляемые соответственно по формулам (18),
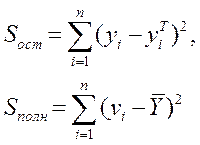 (18)
(18)
где
![]() - данные
эмпирические значения признака Y,
- данные
эмпирические значения признака Y,
![]() - теоретическое
значение признака Y.
- теоретическое
значение признака Y.
Обычно коэффициент детерминированности лежит между 0 и 1. Чем ближе этот коэффициент к 1, тем лучше найденная линия регрессии представляет экспериментальные данные, положенные в основу расчётов.
3. Подготовка теста.
В качестве теста используем результаты ручного счёта. Тест состоит из построения корреляционной таблицы, нахождения уравнений регрессии, и вычисления коэффициента детерминированности.
3.1 Построение корреляционной таблицы.
В этом разделе представлена сама корреляционная таблица и расчёты, необходимые для её заполнения. Некоторые ячейки таблицы заполнялись вручную. При заполнении таблиц использовался Мастер функций. Все действия расписаны поэтапно.
По условию поставленной задачи корреляционная таблица должна состоять из 5 – 6 интервалов, тогда по формуле (2) вычисляем длину каждого интервала. Для определения числа интервалов (k) вводим формулу: 1+3,2*LOG10(30).
Вспомогательная таблица Таблица 3
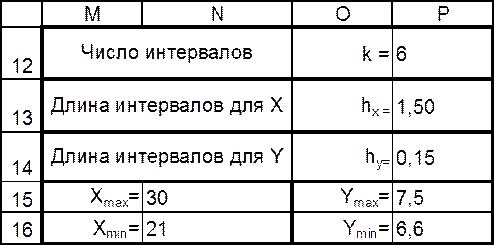
Комментарии к таблице 3.
В ячейку P12 вносим знак «=». Набираем формулу: 1+3,2*LOG10(30). Ввод формулы завершаем нажатием клавиши «Enter».
В ячейку P13 вносим знак «=». Набираем формулу: (N15-N16)/P12. Ввод формулы завершаем нажатием клавиши «Enter».
В ячейку P14 вносим знак «=». Набираем формулу, Набираем формулу: (P15-P16)/P12. Ввод формулы завершаем нажатием клавиши «Enter».
В ячейку N15 вносим знак «=». Набираем формулу: МАКС(А23:А52). Ввод формулы завершаем нажатием клавиши «Enter».
В ячейку N16 вносим знак «=». Набираем формулу: МИН(А23:А52). Ввод формулы завершаем нажатием клавиши «Enter».
Аналогичную операцию выполняем для ячеек P15, P16.
Далее, также с помощью табличного процессора Excel, производим расчёт данных для построения корреляционной таблицы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.