Дальше эту формулу копируем в ячейки G24:G52
Расчеты по негрупповой регрессии Таблица 7
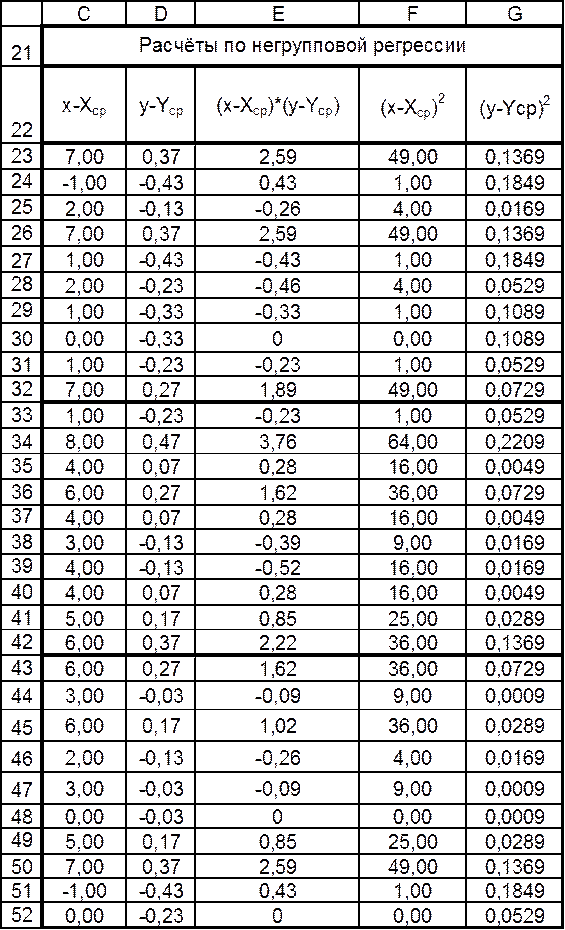
В ячейку E55 заносим знак «=». Вызываем Мастер функций. Выбираем функции СУММ(E23:E52). Ввод формулы завершаем нажатием комбинации клавиш «Ctrl+Shift+Enter».
В ячейку I52 заносим знак «=». Вызываем Мастер функций . Выбираем функции E55/(КОРЕНЬ(СУММ(F23:F52)*СУММ(G23:G52))). Ввод формулы завершаем нажатием комбинации клавиш «Ctrl+Shift+Enter».
Полученное значение:
Коэффициент корреляции в Excel Таблица 8
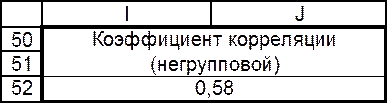
Уравнение регрессии для данных, необъединённых в группы.
Аналогично подпункту 2.2.1. уравнение регрессии составляется с помощью
коэффициента корреляции и величин ![]() .
.
С помощью формул (6) находим среднее значение X и Y:
![]()
![]()
Затем по формуле (5) высчитываем коэффициент корреляции:
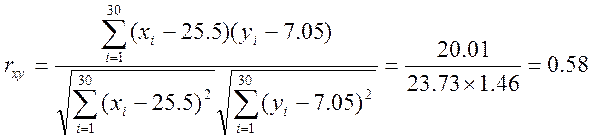
По формуле (10) вычисляем значения величин ![]() :
:
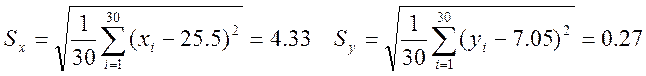
Подставляем все найденные величины в уравнение (9) и преобразуем данное уравнение к нормальному виду:
y = 0,58*0,062(x-25,433)+7,03
Действия при расчёте коэффициента корреляции по группированным данным.
Уравнение регрессии для группированных данных.
Для нахождения уравнения регрессии необходимо рассчитать коэффициент корреляции. В случае с группированными данными коэффициент корреляции вычисляется по формулам (7) и (8). Описание действий в пошаговое. Используется Мастер функций.
Коэффициент корреляции в Excel Таблица 9
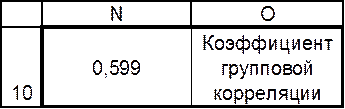
Для составления уравнения регрессии также необходимо найти
величины ![]() . Они вычисляются по формуле (11).
. Они вычисляются по формуле (11).
В ячейку M38 вносим знак «=». С помощью Мастера функций набираем формулу =КОРЕНЬ(СУММ(U3:U8)/30). Ввод формулы завершаем нажатием комбинации клавиш «Ctrl+Shift+Enter».
В ячейку M39 вносим знак «=». С помощью Мастера функций набираем формулу =КОРЕНЬ(СУММ(V3:V8)/30). Ввод формулы завершаем
нажатием комбинации клавиш «Ctrl+Shift+Enter».
Коэффициент корреляции в Excel Таблица 10
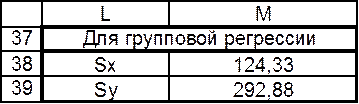
Подставляя данные значения в уравнение (9) и преобразуя его, получаем уравнение регрессии для данных, объединенных в группы:
y = 0,599*2,3518(x-25,5)+7,05 (9)
3. Нахождение уравнения регрессии методом наименьших квадратов.
Для нахождения уравнения регрессии методом наименьших квадратов воспользуемся формулой (15). Для составления обратной матрицы и умножения её на матрицу B воспользуемся Excel.
Операции с матрицами в Excel Таблица 11
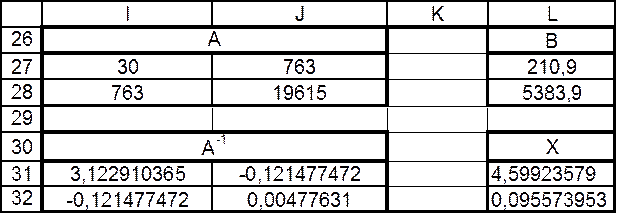
Пояснения к таблице 6:
Для составления матриц А и В необходимо посчитать суммы коэффициентов согласно уравнению (16). В электронной таблице это будет выглядеть следующим образом:
J27=СУММ(B2:K2;B4:K4;B6:K6)
I28=СУММ(B2:K2;B4:K4;B6:K6)
J28=СУММ(B2:K2*B2:K2;B4:K4*B4:K4;B6:K6*B6:K6)
L27= СУММ(B3:K3;B5:K5;B7:K7)
L28=СУММ(B2:K2*B3:K3;B4:K4*B5:K5;B6:K6*B7:K7)
Для нахождения обратной матрицы для матрицы А воспользуемся функцией МОБР. Для этого выделим ячейки I31:I32. Введём в строке формулу:=МОБР(I27:J28).
Затем комбинацией клавиш Ctrl+Shift+Enter закрепим данную формулу во всём массиве.
Для нахождения матрицы Х нужно умножить обратную матрицу А на матрицу В. Воспользуемся функцией МУМНОЖ. Выделим ячейки L31:L32, затем введём формулу:
=МУМНОЖ(I31:J32;L31:L32)
Закрепим формулу клавишами Ctrl+Shift+Enter.
В результате выполненных действий получено два коэффициента уравнения, подставляя их в формулу (12) получаем уравнение регрессии найденное методом наименьших квадратов:
y = 0,0956X + 4,5992
3.3. Вычисление коэффициента детерминированности.
Для вычисления коэффициента детерминированности для данных трёх уравнений воспользуемся формулами(17) и (18).
1. Вычисление коэффициента детерминированности по уравнению для группированных данных:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.