Использование современной компьютерной техники и программного обеспечения для определения зависимости температуры раствора от величины pH раствора, страница 3

      в группы;

·  средние арифметические значения признаков X и Y по группированным данным;

·  величины  по группированным данным;

·  величины  по негруппированным данным;

·  коэффициент корреляции по данным, не объединённым в группы;

·  коэффициент корреляции по группированным данным;

·  наибольшее и наименьшее значение X и Y, длину интервала по X и Y;

·  коэффициент детерминированности;

2. Теоретические сведения.

В этом подразделе содержится информация, необходимая для решения поставленной задачи в общем виде.

2.1 Построение корреляционной таблицы.

Для построения корреляционной таблицы результаты наблюдений по каждому признаку Y и Х разбивают на интервалы, число которых можно определить по формуле

                                                                          (1)

где k -число интервалов, n - число наблюдений соответствующего признака. Далее находят длину интервала, например,

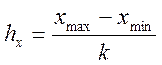                               ,                                           (2)

где  - наибольшее и наименьшее значения признака Х соответственно, k-число интервалов, -длина интервала по признаку X.

Общий вид корреляционной таблицы                           Таблица 2

				…		…
				…		…
				…		…
…..		…..	…..	…	…..	…	…..	…	…..
				…		…
…..	…	…..	…..	…	…..	…	…..	…	…..
				…		…
				…		…
				…		…

 - середины интервалов по признакам Х и Y соответственно,

(, где k - число классов);

 - число наблюдений, попавших в интервал j по признаку Y и в интервал i по признаку X;

 - число наблюдений, попавших в интервал i по признаку X;

 - число наблюдений, попавших в интервал j по признаку Y;

 - условные средние значения признака Y для наблюдений, из интервала i по признаку X;

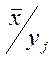 - условные средние значения признака Х для наблюдений, из интервала j по признаку Y;

п - число наблюдений, .

В верхней строке и в первом столбце корреляционной таблицы указаны интервалы по признакам Х и Y соответственно. Во второй строке и во втором столбце таблицы указаны середины интервалов по признакам Х и Y. Подсчитывают число наблюдений, попавших в определённые интервалы по признакам Х и Y по формуле:

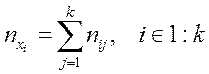
                                                                                    (3)

где k-число интервалов.

В нижней строке и в последнем столбце таблицы представлены условные средние

значения, вычисленные по формулам:

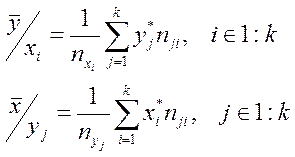                                                                          (4)

2.2 Вычисление коэффициента корреляции, нахождение уравнения регрессии.

Коэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо, в среднем, может быть представлена одна из величин в виде линейной функции от другой.

Коэффициент корреляции вычисляется по формуле

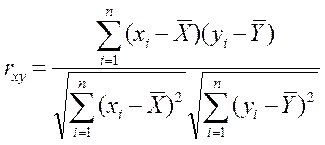                                                                          (5)

где - средние арифметические значения Х и Y соответственно, вычисляемые по формулам:

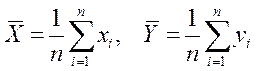                                                                      (6)

а  - значения Х и Y в i-ом наблюдении .

Отметим, что вычисления по формулам (5) и (6) производятся по данным, не объединённым в группы