Задачи линейного программирования

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

НГТУ

Кафедра ВТ

Математические методы системного анализа

Контрольная работа

            Факультет:                 АВТ

            Группа:                      АМ-79

            Студент:                     Монастырский Н.

            Преподаватель:         Казанская О.В.

Новосибирск-2001

Задачи линейного программирования

М 1

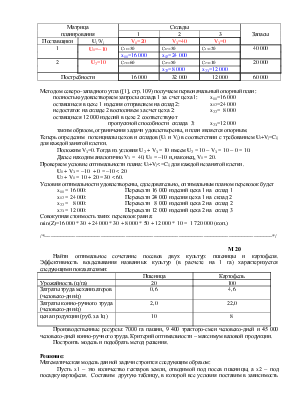
Составить суточный рацион для коров живым весом 400 кг. Суточный удой составляет 10л. молока. Рацион для такой коровы должен содержать 9 кг. кормовых единиц, 960 г переваримого протеина, 370 мг. каротина. Рацион составляется из четырех видов кормов: сена, кукурузного силоса, концентратов и сахарной свеклы.  В 1 кг. этих кормов содержится:

Критерий оптимальности – минимум стоимости рациона.

	Сено	Силос	Концентраты	Сахарная свекла
Кормовые единицы (кг)	0,4	0,2	1,0	0,25
Переваримый протеин (г)	50	10	100	12
Каротин (мг)	20	15	1,0	0
Цена 1 кг. (коп.)	1,0	0,5	2	1,5

Построить модель и подобрать метод решения.

Решение:

Построим математическую модель.

Обозначим x1, x2, x3, x4 соответственно количества сена, силоса, концентратов и свеклы в суточном рационе (в килограммах). Для  того, чтобы рацион был полноценным, должны выполняться уравнения:

0.4x1+0.2x2+1.0x3+0.25x4=9 - т.е. в результирующем рационе мы должны иметь 9 кг кормовых единиц, которые распределены по различным видам кормов в указанных массовых долях.

Точно так же для протеина

50x1+10x2+100x3+12x4=960 (грамм - (г/кг)*кг=г)

и каротина

20x1+15x2+1.0x3+0x4=370

Минимизировать нам нужно общую стоимость суточного корма, т.е. линейную функцию

z=1.0x1+0.5x2+2.0x3+1.5x4

            Получили мат. модель:

            Система ограничений:

0.4x1+0.2x2+1.0x3+0.25x4=9

50x1+10x2+100x3+12x4=960

20x1+15x2+1.0x3+0x4=370

            Минимизируемая функция:

                        z=1.0x1+0.5x2+2.0x3+1.5x4

            В векторном виде:

                        ограничения:

A1x1+A2x2+A3x3+A4x4=A0, где

                                                A1=(0.4, 50, 20)^T, A2=(0.2, 10, 15) ^T,

A3=(1.0, 100, 1.0) ^T, A4=(0.25, 12, 0) ^T, A0=(9, 960, 370) ^T

                                    минимизируемая функция:

                                                z=(C,X), где

                                                C=(1.0, 0.5, 2.0, 1.5) ^T,  X=(x1, x2, x3, x4) ^T

Для решения этой задачи линейного программирования воспользуемся симплексным методом, в изложении [1] (стр. 51) :

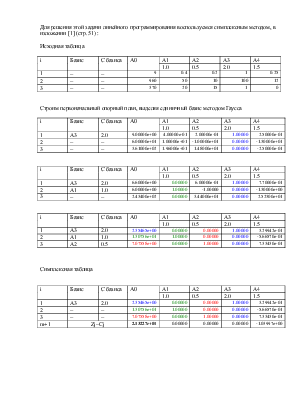
Исходная таблица

i	Базис	С базиса	А0	A1	A2	A3	A4
				1.0	0.5	2.0	1.5
1	-	-	9	0.4	0.2	1	0.25
2	-	-	960	50	10	100	12
3	-	-	370	20	15	1	0

Строим первоначальный опорный план, выделяя единичный базис методом Гаусса

i	Базис	С базиса	А0	A1	A2	A3	A4
				1.0	0.5	2.0	1.5
1	A3	2.0	9.00000e+00	4.00000e-01	2.00000e-01	1.00000	2.50000e-01
2	-	-	6.00000e+01	1.00000e+01	-1.00000e+01	0.00000	-1.30000e+01
3	-	-	3.61000e+02	1.96000e+01	1.48000e+01	0.00000	-2.50000e-01

i	Базис	С базиса	А0	A1	A2	A3	A4
				1.0	0.5	2.0	1.5
1	A3	2.0	6.60000e+00	0.00000	6.00000e-01	1.00000	7.70000e-01
2	A1	1.0	6.00000e+00	1.00000	-1.00000	0.00000	-1.30000e+00
3	-	-	2.43400e+02	0.00000	3.44000e+01	0.00000	2.52300e+01

i	Базис	С базиса	А0	A1	A2	A3	A4
				1.0	0.5	2.0	1.5
1	A3	2.0	2.35465e+00	0.00000	0.00000	1.00000	3.29942e-01
2	A1	1.0	1.30756e+01	1.00000	0.00000	0.00000	-5.66570e-01
3	A2	0.5	7.07558e+00	0.00000	1.00000	0.00000	7.33430e-01