Задачи линейного программирования, страница 2

Симплексная таблица

i	Базис	С базиса	А0	A1	A2	A3	A4
				1.0	0.5	2.0	1.5
1	A3	2.0	2.35465e+00	0.00000	0.00000	1.00000	3.29942e-01
2	-	-	1.30756e+01	1.00000	0.00000	0.00000	-5.66570e-01
3	-	-	7.07558e+00	0.00000	1.00000	0.00000	7.33430e-01
m+1	Zj-Cj		2.13227e+01	0.00000	0.00000	0.00000	-1.03997e+00

Мы решаем задачу минимизации. В этом случае отсутствие в строке m+1 положительных оценок для векторов A1, A2, A3 и A4 говорит, что уже найден оптимальный план:

X=(13.0756, 7.07558, 2.35465, 0) ^T,

соответствующее значение функции

z= ((13.0756, 7.07558, 2.35465, 0)^T, (1.0, 0.5, 2.0, 1.5) ^T) = 21.3227

Итак, рацион нужно составлять следующим образом:

Корм	Цена, коп.	Кол-во, кг*	Стоимость, коп.*
Сено	1.0	13.0756	13.0756
Силос	0.5	7.07558	3.53779
Концентрат	2.0	2.35465	4.7093
Сах. свекла	1.5	0	0
Итого		22.50583	21.32269

* - при больших объемах закупок имеет смысл рассматривать дробную часть.

/*-------------------------------------------------------------------------*/

М 10

Предприятие имеет 2 цеха и 3 склада. Цех 1 производит за определенное время 40 тыс. шт. и цех 2 – 20 тыс. шт. одинаковых изделий. Пропускная способность складов предприятия: склад 1 – 16 тыс. шт.;  склад 2 – 32 тыс. шт.; склад 3 – 12 тыс. шт. Стоимость перевозки единицы изделий: из цеха 1 на склад 1 – 30 коп., на склад 2 – 30 коп., на склад 3 – 20 коп, из цеха 2 на склад 1 – 60 коп., на склад  2 -  50 коп., на склад 3 – 10 коп.

Определить наиболее рациональную систему перевозки продуктов каждого из цехов, позволяющую достигнуть минимума расхода на транспортировку.

Построить модель и подобрать метод решения.

Решение:

            Имеем классическую замкнутую (общее количество продукции у поставщиков равно суммарным нуждам  потребителей) транспортную задачу. Математической моделью такой задачи является совокупность

ограничений

           

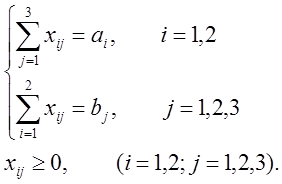
где x_ij - это количество груза, доставляемых из цеха i на склад j, a_i - количество изделий, подлежащих вывозу из цеха № i, b_j - пропускная способность j-го склада.

и функции 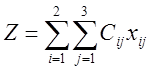, где С_ij - стоимость перевозки одного изделия из цеха № i  на склад № j. Минимум min(Z) функции Z на множестве x_ij, допускаемом ограничениями, дает нам наименьшую стоимость перевозок. Этой стоимости можно достичь, если избрать план перевозок, соответствующий такой комбинации x*_ij, что  .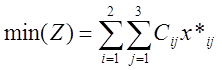

Для решения задачи выберем метод потенциалов ([1], стр. 113)

            Построим матрицу планирования:

Матрица планирования		Склады			Запасы
		1	2	3
Поставщики	Ui\Vj	V1=20	V3=40	V3=0
1	U1=-10	С11=30	С12=30	С13=20	40 000
		x11=16 000	x12=24 000
2	U2=10	С21=60	С22=50	С23=10	20 000
			x22=8 000	x23=12 000
Постребности		16 000	32 000	12 000	60 000