Задачи линейного программирования, страница 5

                                    . . .

                                    an1*x1+an2*x2<=bn; x1,x2>=0;

определяет многоугольник допустимых решений на плоскости.  Необходимо отыскать точку, в которой достигается минимальное на этом многоугольнике значение рассматриваемой линейной функции.

Теорема ([1], стр. 40)

Линейная функция задачи линейного программирования достигает своего минимального(максимального) значения в угловой точке многогранника решений. Если линейная функция принимает минимальное(максимальное) значение более, чем в одной угловой точке, то она достигает того же  значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Пусть нужно найти минимум функции z=c1*x1+c2*x2. Зафиксировав z, будем иметь уравнение прямой линии. Вдоль этой линии значение линейной комбинации c1*x1+c2*x2 постоянно и  равно z. Как следует из теоремы, имеет смысл рассматривать положения прямой в которых она становится опорной для многоугольника решений. Минимальное из значений, которые при этом принимает z и будет искомым. Пересечение прямой и многоугольника даст нам решение задачи линейного программирования.

Задача 1

z = x1+x2 ® max

  - x1+ 4x2 ³ 6

    x1+ x2   £ 3

           xj ³ 0

Построим многоугольник решений, для чего в системе координат  x1Ox2 на плоскости изобразим граничные прямые

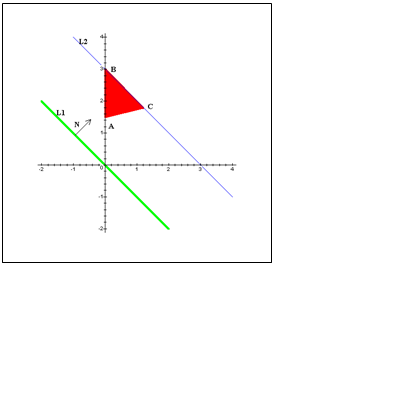            -x1+4x2=6 (AB), x1+x2=3 (BC), x1=0 (DA), x2=0 (CD). Взяв какую-нибудь точку в качестве пробной определим полуплоскости соответствующие неравенствам. В результате получим треугольник ABC. Прямая z = x1+x2, при z=0, показана на рисунке как L1. При ее перемещении в направлении N параллельно самой себе она дважды оказывается опорной для ABC: когда проходит  через  точку A и когда накладывается на отрезок BC (положение L2). Очевидно, в точках прямой L2 функция z достигает своего максимума, следовательно любая из точек отрезка BC будет решением исходной задачи. Выразим это множество точек аналитически. Для этого найдем сначала координаты точек B и С.

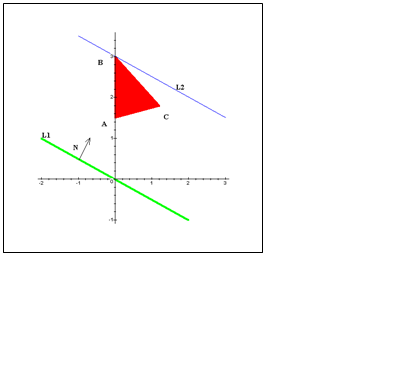
B лежит на пересечении прямой BC (x1+x2=3) и оси Ox2, поэтому B=(0,3). С - точка пересечения линий BC и CA (-x1+4x2=6), следовательно ее координаты можно определить,  решая систему уравнений:

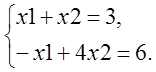    Получаем B=(1.2, 1.8).

Итак,

решением Задачи 1 будет любая из точек множества M={(x1,x2): 0<=x1<=1.2, x2=3-x1}, значение максимизируемой функции в этих точках равно 3.

Задача 2

z = x1 +2x2 ® max

  - x1+ 4x2 ³ 6

     x1+ x2   £ 3

             xj ³ 0

Действуя совершенно так, как при решении Задачи 1, получим, что функция z максимальна в точке

B=(1,3), при тех же допустимых значениях, что и в Задаче 1 (треугольник ABC). z(B)=6.

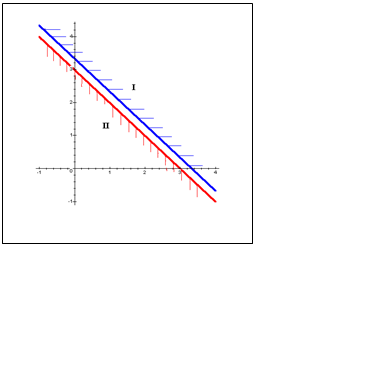Задача 3

z = x1+2x2 ® min

     3x1+ 3x2 ³ 10 (I)

     x1+ x2   £ 3                (II)

   - x1+ 4x2 ³ 6    (III)

              xj ³ 0

Система ограничений в этой  задаче несовместна, а  именно условия I и II противоречат друг другу, что  отлично  демонстрирует рисунок.

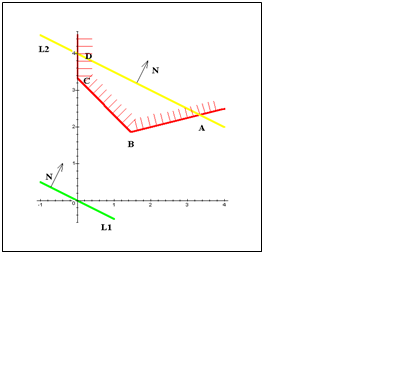Задача 4

z = x1+2x2 ® max

      3x1+ 3x2 ³ 10

       - x1+ 4x2 ³ 6

                  xj ³ 0

В этом случае многоугольник  решений не ограничен, функция z ограничена  на нем только снизу, в то время как нам нужно найти   ее максимум.

Можем сделать следующее заключение:

максимального значения  функция  z на многоугольнике решений, определяемом совокупностью ограничений не имеет, а потому и Задача 4 не имеет решения.

Литература

1. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б., Математическое программирование. М, 1980.