Задачи линейного программирования, страница 4

Аналогично

(II) 40*x1 + 2200*x2 <= 45000 - не более 45000 человеко-дней конно-ручного труда

(III) x1 + x2 <= 7000 - не более 7000 га пашни

Очевидно, что должно быть

(IV) x1,x2>=0.

Нужно, чтобы  выручка от продажи произведенных продуктов была макcимальна  при имеющихся ресурсах, поэтому соответствующая задача линейного программирования (ЗЛП) ставится как задача максимизации функции выручки:

                        Z = 200*x1 + 800*x2 (V), где x1,x2 удовлетворяют условиям (I)-(IV)

Метод решения:

            Ввиду того, что мы оперируем здесь с двумя переменными, очень привлекательным является графический метод решения ЗЛП ([1], стр. 44, также см. эту работу ниже). Как известно, каждое из наших ограничений определит  некоторую полуплоскость на координатной плоскости x2Ox1. Пересечение этих полуплоскостей образует множество допустимых точек, на котором и минимизируется функция Z. Затруднения вызывает отображение необходимых объектов в масштабе, что объясняется несоразмерностью коэффицентов в неравенствах. На  самом же деле, вполне окажется достаточным  набросок сложившейся картины,  который  покажет взаимное расположение объектов. Дальнейшее ясно из рисунка.

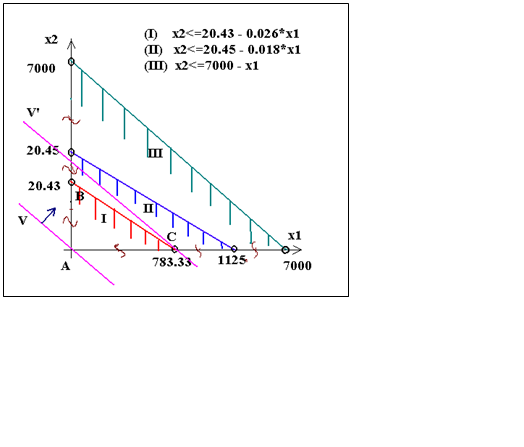
 Вся совокупность ограничений сводится  к неравенствам (IV) и неравенству (I), относящемуся к труду механизаторов. Нехватка этого ресурса по сравнению с размером пашни чрезвычайна. Однако, будем исходить из того, что есть.

(V) при постоянном Z представляет собой уравнение прямой:

x2=Z/200 - (0.25)*x1.

Изобразим на рисунке положение такой прямой при Z=0. Учтем при этом геометрический смысл коэффициента при x1: таковой коэффициент  в (I) меньше соответствующего коэффициента в (V), поэтому (V) будет иметь  более крутой наклон. Теперь будем  перемещать новую прямую перпендикулярно самой себе так, находя все возможные положения этой прямой, в которых она будет опорной(см. теор. пояснения к решениям графич. задач ниже) по отношению к многоугольнику ABC допустимых решений. Из всех опорных положений остановимся на том, в котором прямая проходит через ось Ox2 как можно выше, что  будет соответствовать максимальному значению Z. Оптимальное положение прямая (V) занимает при прохождении через точку С. Больше ни одна из точек ABC не совпадает с данной прямой в этом положении, поэтому задача имеет единственное решение:

            x1 = 783.33, x2 = 0.

Возвращаясь к смыслу, заложенному в эти переменные, заключаем:

Для того, чтобы получить максимальную отдачу имеющихся ресурсов, следует засеять 783.33 га пшеницей, а картофель  не садить вообще. При этом мы получим

783.33га * 20ц/га = 15666.6ц зерна,

которое при реализации обратится выручкой в размере

                                                15666.6ц*10р/ц = 156666р.

Решить графически предложенные задачи линейного программирования.

1.

z = x1+x2 ® max

  - x1+ 4x2 ³ 6

    x1+ x2   £ 3

           xj ³ 0

2.

z = x1 +2x2 ® max

  - x1+ 4x2 ³ 6

     x1+ x2   £ 3

             xj ³ 0

3.

z = x1+2x2 ® min

     3x1+ 3x2 ³ 10

     x1+ x2   £ 3 

   - x1+ 4x2 ³ 6

              xj ³ 0

4.

z = x1+2x2 ® max

      3x1+ 3x2 ³ 10

       - x1+ 4x2 ³ 6

                  xj ³ 0

Решение

Принята терминология учебника [1].

Основанием для графического метода решения является геометрическая интерпретация задач линейного программирования. Согласно этой инерпретации совместная система условий вида

                                    a11*x1+a12*x2<=b1

                                    a21*x1+a22*x2<=b2