Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 1

Теоретические исследования работы жестких нитей в двухполюсной радиально - вантовой системе

Основные положения.

Основными несущими элементами в двухполюсной радиально - вантовой системе являются гибкие и жесткие нити.

Жесткой нитью будем называть криволинейный провисающий стержень, имеющий определенную изгибную жесткость, закрепленный концами на опорах и держащий нагрузку, главным образом, благодаря осевому растяжению.

Жесткая нить подобна арке – криволинейному, выпуклому стержню и отличается от нее тем, что арка имеет кривизну, противоположную нити и держит нагрузку в результате сжатия. Поэтому иногда жесткую нить называют обратной аркой. Она имеет определенную форму, полученную или изготовленную, и сопротивляется ее изменению.

Теория жесткой нити является обобщением теории нити, в которой гибкая нить будет представлять частный случай.

При загружении двухполосного радиально - вантового покрытия вертикальной нагрузкой в нитях будут возникать перемещения как в вертикальной, так и в горизонтальной плоскостях. При этом диагональный элемент, связанный с нитями, не дает свободно им перемещаться, от него они получают определенные воздействия, которые будут тем значительнее, чем ближе к опорному контуру находится нить. Для средней нити, если пренебречь этими воздействиями, можно нить рассматривать как бы перемещающейся свободно, не связано с системой, что упрощает ее расчет и исследование.

При расчете свободно провисающих нитей использованы следующие допущения:

1. Рассматриваются нити с малыми стрелками провисания (1/8 пролета и менее). При этом усилия в нити мало меняются по длине, а длина мало отличается от пролета .

2. При действии нагрузок материал нити подчиняется закону Гука.

3. Для нити конечной изгибной жесткости принята техническая теория изгиба  M = - EJ-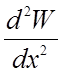

4. Момент инерции относительно вертикального сечения имеет постоянное значение по длине нити.

Для расчета жестких нитей, мы будем использовать методику Н.С.Москалева (      ) . Автором получены формулы для определения прогибов и распоров, которые удобны для практических расчетов, а также позволяют выполнить анализ работы жестких нитей и назначить рациональные параметры.

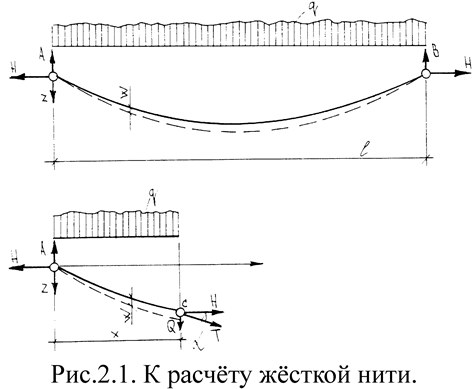Рассмотрим жесткую нить с шарнирными опорами, расположенными на одном уровне. До приложения нагрузки нить имела исходное очертание, соответствующее ординатам Z. Под нагрузкой (рассматривается только вертикально действующая нагрузка) в нити возникает распор H_i и появляются вертикальные перемещения W.

Для вывода уравнения нити конечной изгибной жесткости рассечём нить вертикально в сечении X и составим уравнения равновесия для рассматриваемого участка нити (рис. 2.1). Проектируя силы на ось X , замечаем, что распор во всех сечениях имеет постоянное значение.  Вертикальные реакции опор у жесткой нити не будут отличаться от реакций аналогичной балки. Их определяют по формулам:

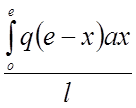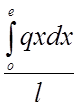A=; B =                                                                                       (2.1)

Проектируя силы на ось  Z , получим уравнение

A - 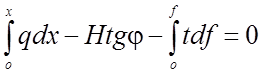 ,                                                                  (2.2)

где A - 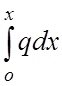 - сумма внешних сил слева;

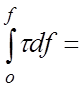Q - сумма касательных направлений, взятая по всему сечению.

Из уравнения (2.2) определяем вертикальную составляющую тяжения Q_ж  она равна Htg- Q_. Тангенс угла наклона тяжения будет

tg =  -  .

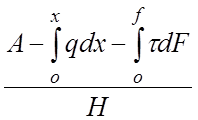Уравнение моментов, взятое относительно точки C, расположенной на оси нити, имеет вид

A_х - 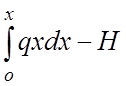_ж ( z + w ) - m = 0                                                           ( 2.3 )

где  A_x - 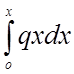 - момент, равный изгибающему моменту в аналогичной балке , m-момент, изгибающий нить.

Решая уравнение ( 2.3 ) относительно распора , получим

H=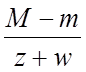

Тяжение находим из формулы

T=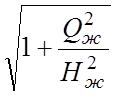

Момент m, изгибающий нить, можно определить, пользуясь приближенной теорией изгиба прямолинейных брусьев. Кривизну нити ввиду пологости не учитываем .

Тогда m= - E J w" ,

где EJ - изгибная жесткость нити, причем момент инерции взят относительно вертикального сечения; w" - вторая производная прогиба.

Выражение (2.3) приобретает вид уравнения прогибов, известного из теории висячих мостов:

E J w" - H(z + w) + M = 0                                                                     (2.4)

Уравнение (2.4) описывает не исходное, а деформированное состояние жесткой нити. Оно не будет иметь решения до тех пор, пока распор не станет известен. В теории висячих мостов нахождение распора составляет одну из основных трудностей расчета, в связи с чем разработано много методов для его определения. Воспользуемся уже известной из теории нити формулой длины кривой в силовой трансформации, которая  является дополнительным уравнением, недостающим при решении. Под нагрузкой нить удлиняется на величину DS и выражение получит вид: