Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 4

Начальные ординаты нити, имеющей в середине пролета стрелку f изменяются по закону:

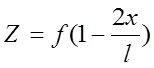                                                                                          (2.83)

Сопряжение нити с диагональным элементом принимаем жестким и шарнирным.

Общее решение дифференциального уравнения для нити на рис.2.16 будет:

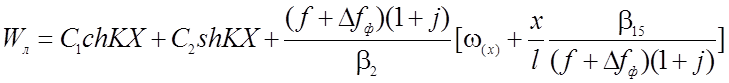;      (2.84)

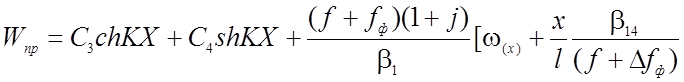]             (2.85)

Постоянные интегрирования находятся из условия:

при x=l/2® W_л=W_пр=0 , при x=0® W_л=W_пр=Df_ф.

Подставляя в (2.84), (2.85) значения постоянных коэффициентов, будем иметь:                                                

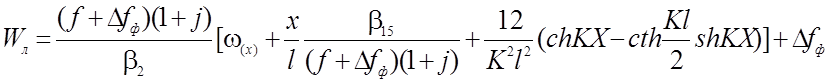   (2.86)

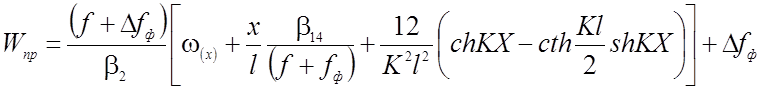    (2.87)

Входящие в формулы коэффициенты b₁ , b_{2 ,} b_{14 ,}b₁₅  приведены в таблице 2.6.

Для нити, не имеющей в центре шарнира, решения для прогибов в общем случае загружения даны в таблице 2.6.

Полагая коэффициенты j, j₁, j₂ или один из них равными нулю, получаем частные решения, которые приведены в таблицах 2.7, 2.8, 2.9, 2.10.

Для определения фиктивного прогиба в середине пролета или, что тоже самое, распора Н, используем уже известную формулу, но учитываем, что.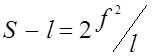

Величины М_d, h ₁ ,h₂ , D_r, входящие в формулу, заменяем значениями, которые они имеют для данного вида загружений ( табл. 2.1, 2.7, 2.8, 2.9, 2.10).

Выполним анализ работы жесткой нити из прямолинейных элементов на различные виды загружения.

а) Нить загружена расчетной нагрузкой , коэффициенты j₁, j₂ равны нулю.

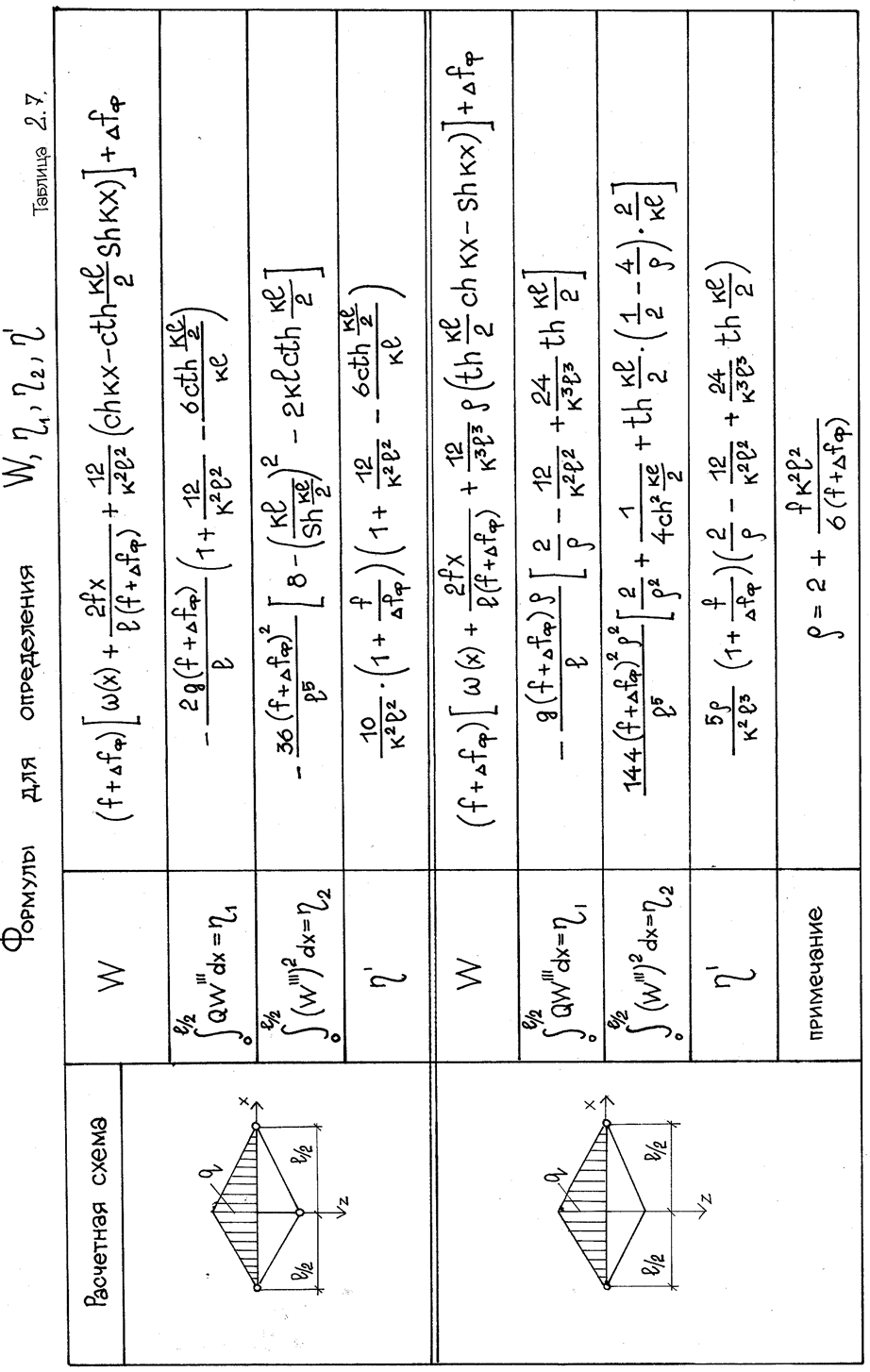
Формулы для определения прогибов двух шарнирной и трех шарнирной нити приведены в табл. 2.7.

Фиктивный прогиб (Df_ф) определяется из уравнения:

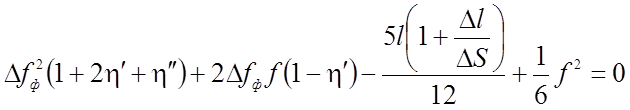                      (2.88)

Коэффициенты h¹и h²принимаются по таблице 2.7 в зависимости от расчетной схемы. Для практических вычислений можно пользоваться приближенной формулой:

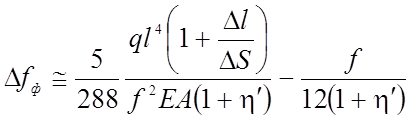                                                     (2.89)

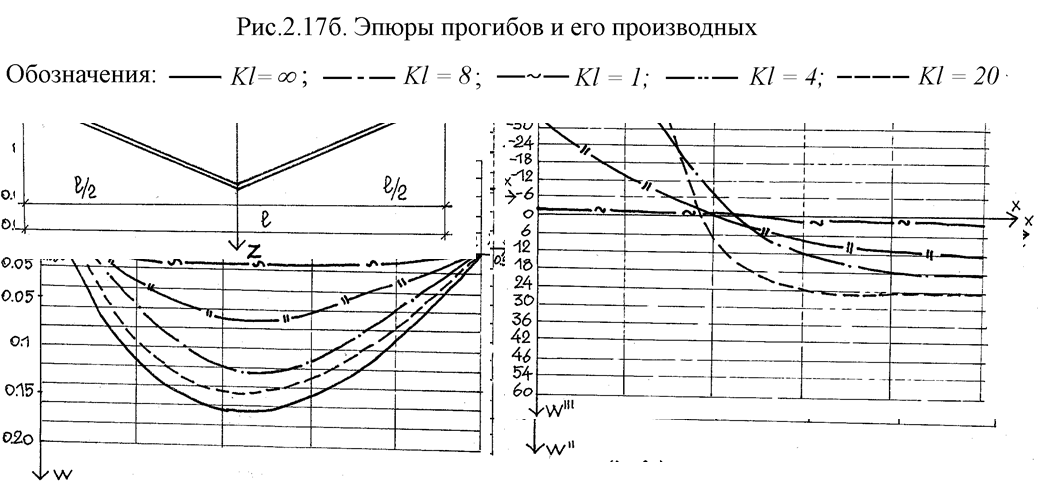
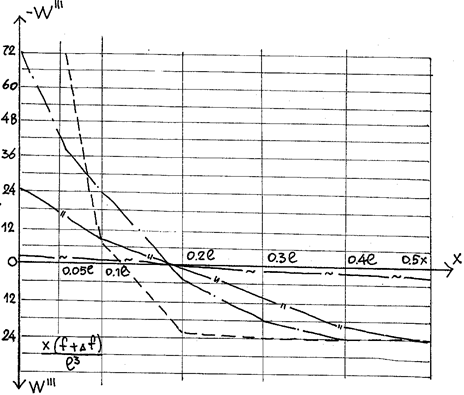
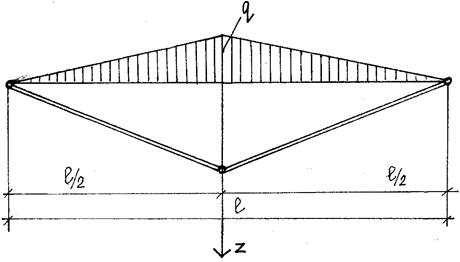
Анализируя полученные решения и эпюры W ( рис. 2.17а, 2.17б) видим, что прогибы зависят от начальной стрелки f. Жесткость EA в данном случае влияет только на величину условного прогиба и даже при нерастяжимой нити прогибы W не стремятся к нулю. При загружении нити полной нагрузкой, она стремится принять очертание близкое к кривой тяжения, при этом в центральной части нити она поднимается вверх. Изгибная жесткость для такой нити существенно влияет на величину прогибов, уменьшая их. Эпюра прогибов W имеет три максимума: один в середине пролета и два в  пролета. Прогиб в середине пролета, равный для трех шарнирной нити условному прогибу, имеет значительную величину. Из рассмотрения формул (2.88 и 2.89) можно подметить одно явление.

Второй член в формуле (2.89) превосходит первый, является величиной отрицательной, зависит от стрелки f. Первый член в формуле (2.89) положительный, зависит от удлинения нити и подвижности опор и обратно пропорционален квадрату начального провеса. Поэтому для данного вида нитей смещение опор и удлинение нити уменьшают прогибы в середине пролета, но при этом прогибы в пролете и изгибающие моменты могут возрастать.

Для определения места максимального прогиба приравниваем нулю первую производную от прогиба. Для различных значений Kl абсцисса максимума приведена на рис. 2.17а, 2.17б.

Изгибающие моменты для трех шарнирной нити определяются из выражений:

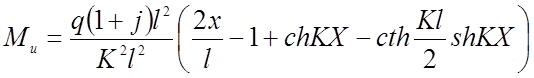                                   (2.90)

Они растут по мере удаления от опоры (рис. 2.17а ), а затем резко падают до нуля в центре, зависят от нагрузки q, а пролета нити и изгибной жесткости. Абсцисса Х, где возможен максимум определяется по формулам (2.21, 2.23, 2.25). Максимальные изгибающие моменты при полном загружении имеют величину:

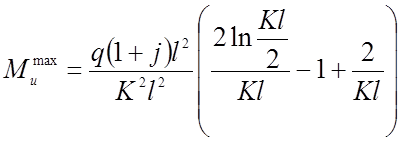                                                      (2.91)

Для симметричного сечения высотой h напряжения от изгиба определяются для верхних фибровых волокон по формуле:

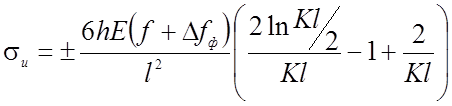                                               (2.92)

Для двух шарнирной нити эпюра W" и, соответственно, изгибающий момент (рис. 2.17б) имеют три максимума: два отрицательных и один положительный, который находится в середине пролета.

Сравнивая максимальные изгибающие моменты, замечаем, что момент с абсциссой Х=0 имеет большое значение, чем другие два.

Его величина определяется из выражения:

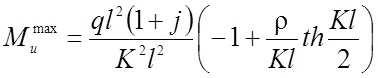                                                          (2.93)

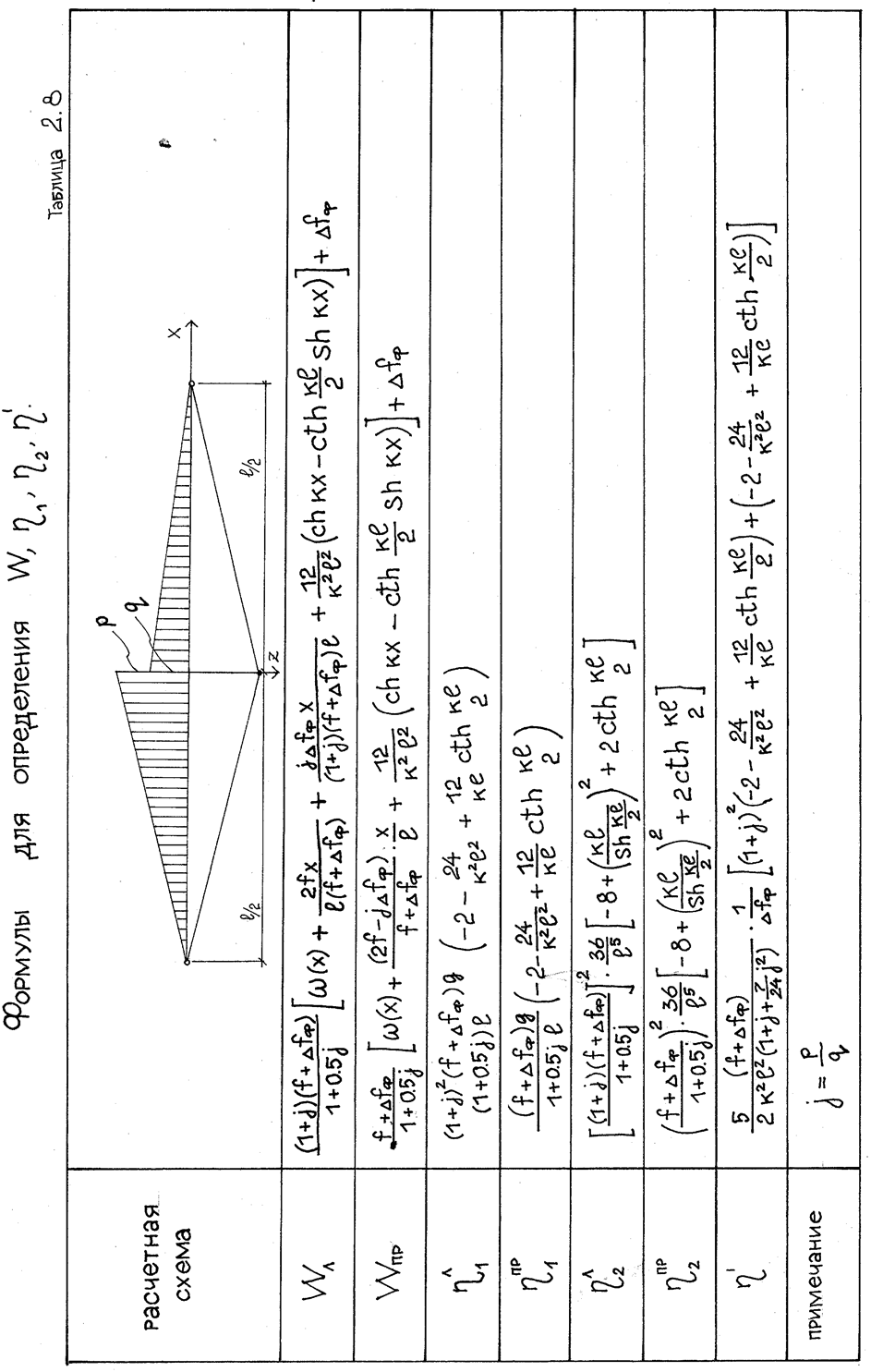
б) Нить загружена постоянной нагрузкой q и временной нагрузкой на половине пролета.

Решения дифференциального уравнения приведены в таблицах 2.8, 2.9.

Квадратное уравнение относительно Df_ф запишется так:                          

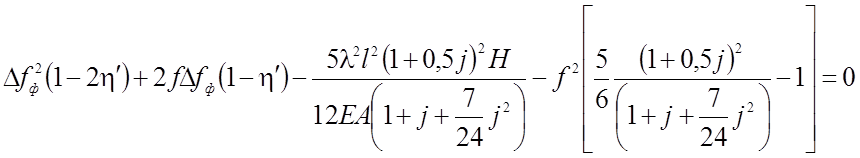    (2.94)

Для двух шарнирной нити:

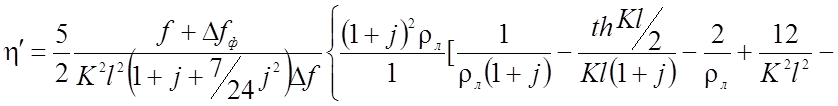
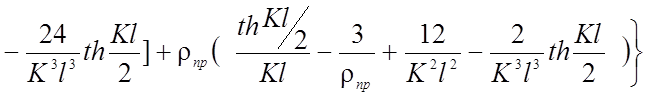
Для трех шарнирной нити значение  дано в таблице 2.8.

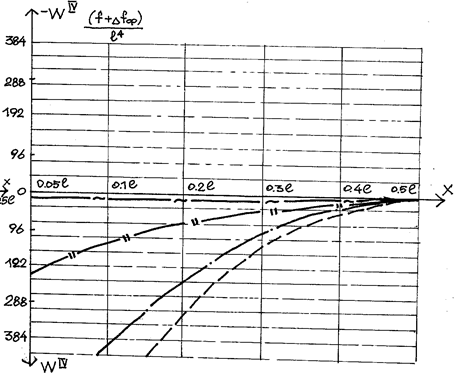
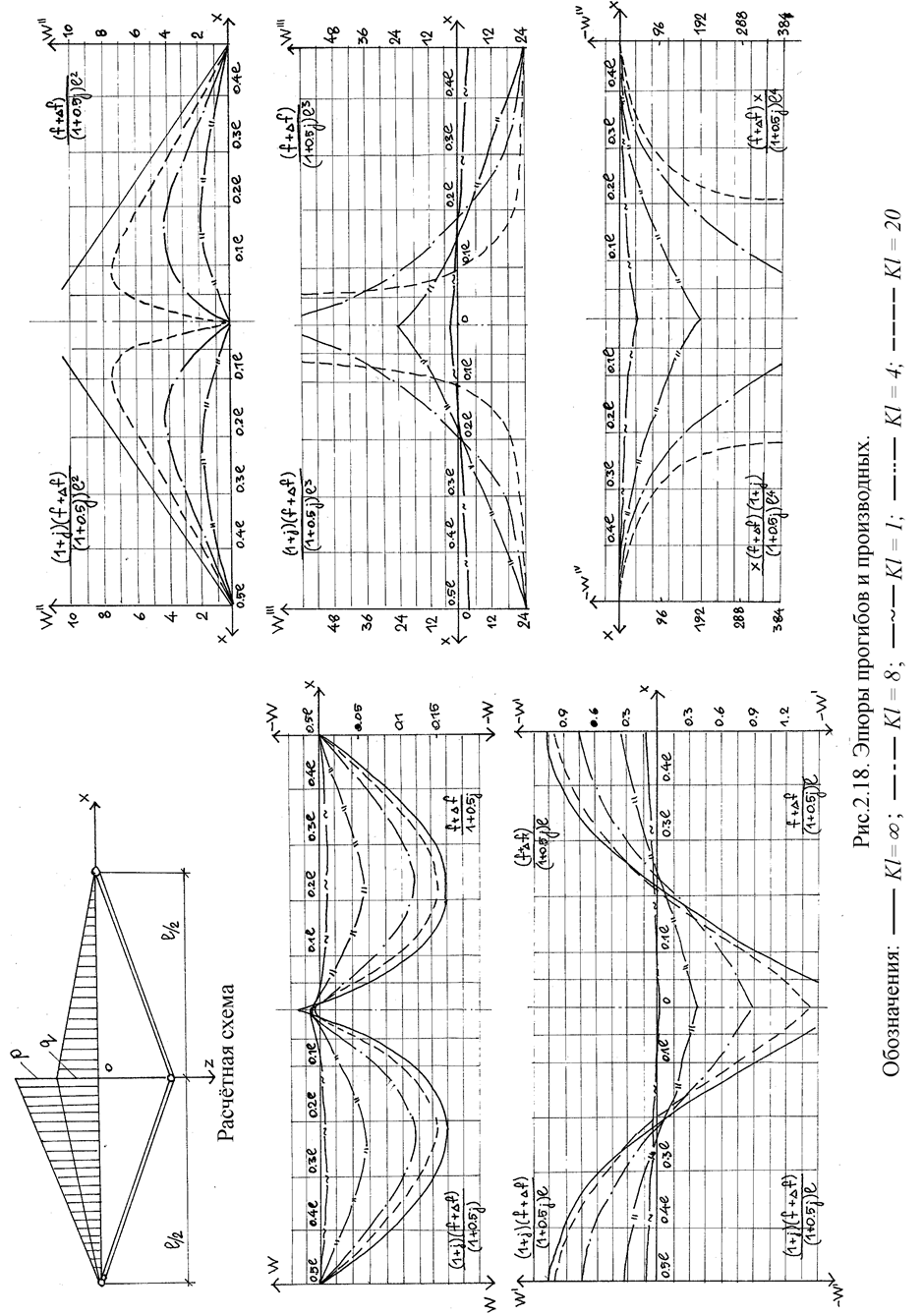
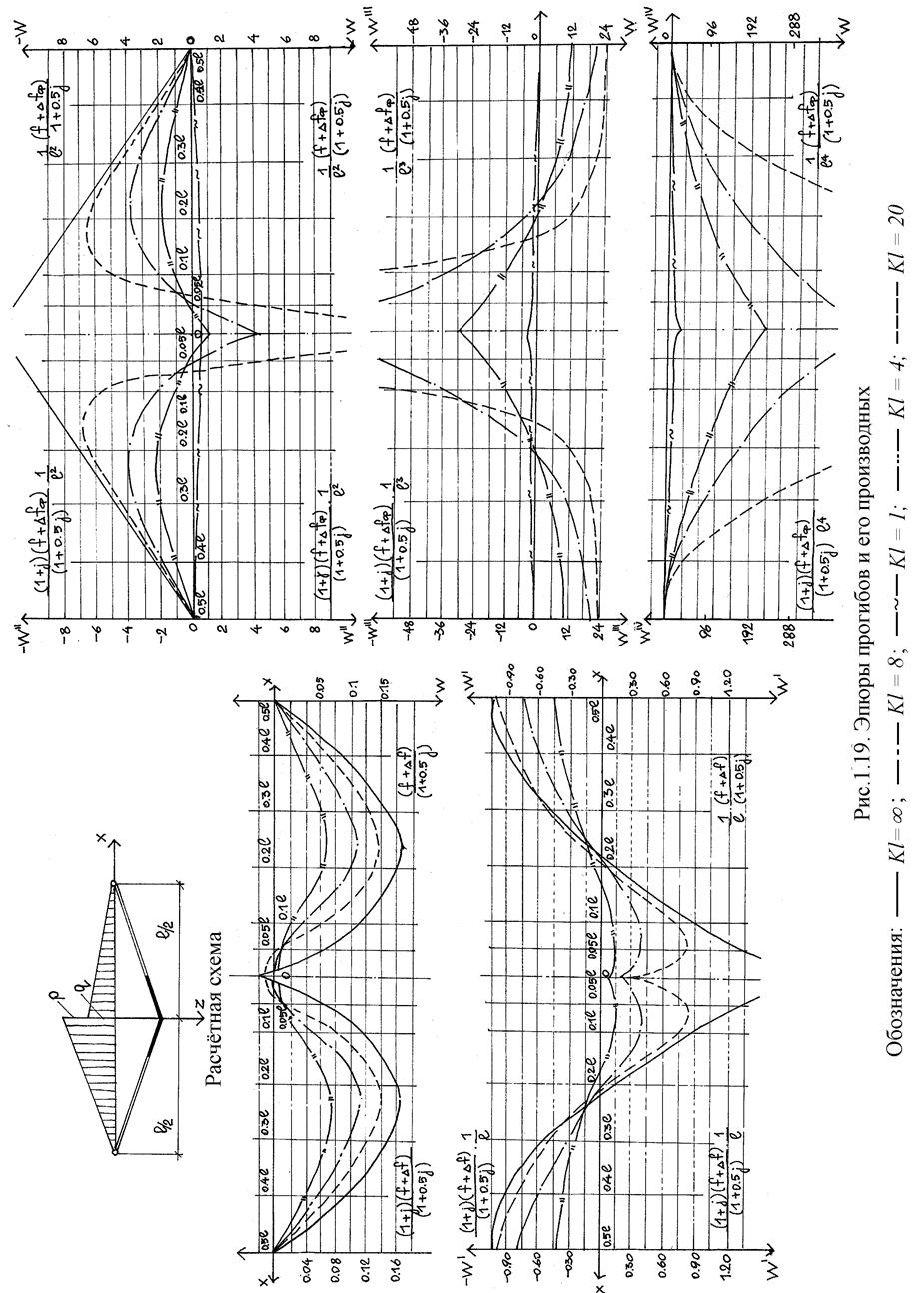
Анализируя формулы (табл. 2.8,2.9),  эпюры W (рис. 2.18, 2.19) замечаем, что прогиб зависит от начальной стрелки f, растяжимая жесткость и смещение опор незначительно влияют на его величину, изгибная жесткость существенно влияет на прогибы, уменьшая их. Как показано на эпюрах, прогибы в нити при загружении половины пролета ее временной нагрузкой аналогичны прогибам при полном загружении, отличаются постоянным коэффициентом, зависящим от отношения временной нагрузки к постоянной, и коэффициентом гибкости Kl.

Выражения для изгибающих моментов в трех шарнирной нити имеют вид:

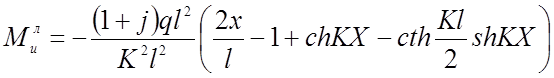                                (2.95)

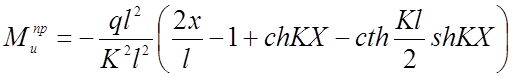                                        (2.96)

Легко видеть, что изгибающие моменты для полного загружения и половинного имеют одинаковый характер. При этом в загруженной половине пролета изгибающие моменты имеют несколько большие значения, чем изгибающие моменты при полном загружении. Это объясняется тем, что при половинном загружении нити временной нагрузкой коэффициент Kl имеет меньшее значение, чем при полном загружении. Изгибающие моменты имеют значительную величину, растут по мере удаления опоры, затем быстро падают до нуля в центре.