Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 4, страница 2

Для двух шарнирной нити изгибающие моменты определяются из выражения:

                          

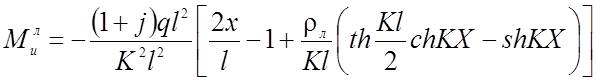
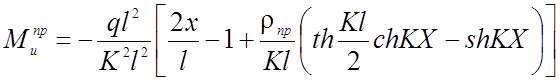                                          (2.97)

Следует отметить, что изгибающие моменты имеют два максимума: один находится примерно в четверти пролета, другой в середине пролета нити. Сравнивая их между собой, видим,  что изгибающий момент в середине пролета нити по абсолютной величине больше изгибающего элемента в четверти пролета.

в) В качестве примера рассмотрим более общий случай загружения нити, приложив наряду с нагрузкой g = q + r в центре пролета нити сосредоточенную силу N. Уравнения прогибов приведены в таблице 2.10.

Дифференцируя дважды уравнения прогибов, получаем для трех шарнирной и двух шарнирной нити соответственно:

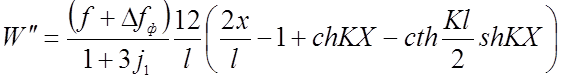                               (2.98)

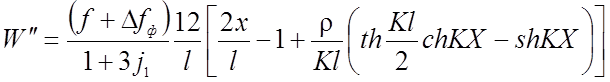
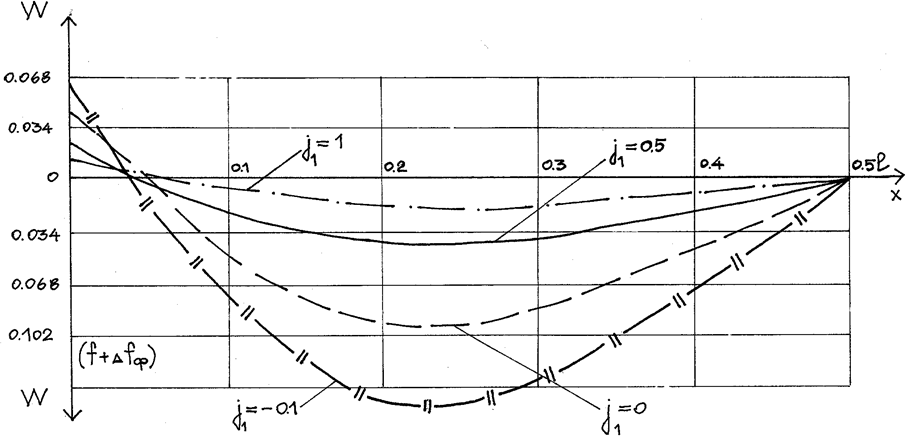
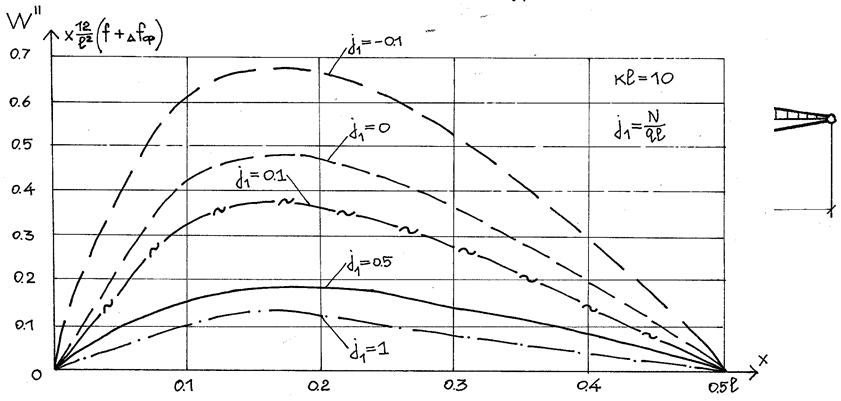
Рассмотрим, как реагирует нить на вертикальную силу N. Предположим, что сила N имеет отрицательное значение, т.е. направлена снизу вверх. Легко убедиться, что прогиб и вторая производная, от действия нагрузки q и силы N теперь будут большими, чем прогиб и вторая производная определенные при силе N=0. Если сила N имеет положительное направление, то в зависимости от отношения j₁ прогибы, а вместе с ними вторая производная могут быть значительно уменьшены (рис.2.20). Это можно объяснить тем, что нагрузка приближается к равновесной для нити данного очертания. В двухполюсной системе сосредоточеная сила появляется в результате взаимодействия нити с диагональным элементом. Выше было доказано, что при загружении покрытия постоянной нагрузкой нить в центральной части пролета поднимается вверх. При этом возникающий прогиб имеет значительную величину. Диагональный элемент препятствует перемещению нити в вертикальном направлении, от него появляется сосредоточенная сила, направленная сверху вниз. Дополнительной силой может быть так же световой фонарь и технологическое оборудование. Так как рассматриваемая сила уменьшает прогибы и изгибающие моменты, то в этом смысле она является полезной.

Сравнивая работу двух шарнирной и трех шарнирной нити, выполненной из двух прямолинейных элементов, заметим, что прогибы их отличаются незначительно. Однако, в двух шарнирной нити в центре пролета возникают изгибающие моменты, превышающие моменты в четвертях пролета. В связи с этим в данном покрытии целесообразно применять нить, имеющею в центре пролета шарнир.

Для выбора ориентировочных геометрических и физических характеристик трех шарнирной жесткой нити рассмотрим напряженное состояние нити при полной равномерно распределенной нагрузке на покрытии (табл.2.7.), так как в этом случае возникает максимальный распор нити Н, а изгибающие моменты отличаются незначительно от загружения, рассмотренного в пункте “б”.

Ограничиваясь нормальными напряжениями, условие прочности запишется в таком виде:

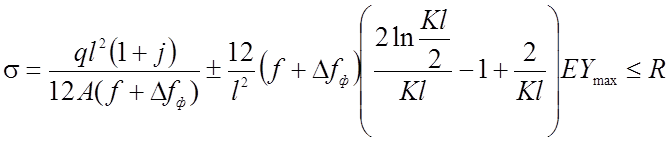                (2.99)

Первый член уравнения содержит напряжения осевого растяжения, второй - краевые напряжения от изгиба в сечении, где действует максимальный изгибающий момент. Из (2.96) видно, что напряжение осевого растяжения и напряжения изгиба зависят от стрелки f.

Исходя из этих соображений может быть назначена высота сечения нити.

Продифференцировав выражение (2.99) по f и выполнив соответствующие преобразования, получим:

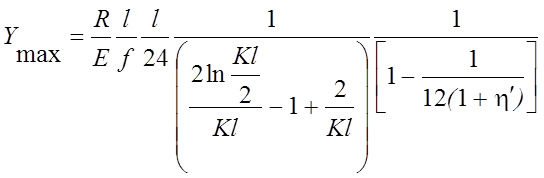                                  (2.100)

При выводе формулы принимали .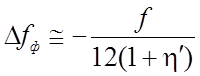

(Первоначально коэффициент h' полагаем равным h'=1.4 - 1.6).

Эта формула является приближенной, но дает возможность определить высоту сечения нити в зависимости от параметра kl, от отношения стрелки к пролету, от расчетного сопротивления. Регулируя отношение стрелки к пролету, физические характеристики нити, всегда можно назначить рациональную высоту сечения.

Требуемый момент инерции подбираем исходя из заданного прогиба и допускаемого искривления по методике, рассмотренной для нити, изогнутой по кубической параболе.

Величина распора Н при полном загружении определяется по приближенной формуле:

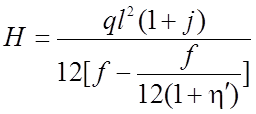                                                                           (2.101)

Зная высоту сечения нити, изгибную жесткость и распор Н, можно определить краевые напряжения изгиба по формуле (2.92).

Для практических расчетов при назначении площади сечения можно пользоваться формулой:

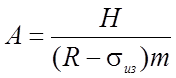                                                                                      (2.102)

где m - коэффициент условия работы,

s_из - краевые напряжения изгиба.

Отметим, что при выводе формул (2.100 - 2.102) рассматривалась нить, не связана с системой, поэтому выбранные параметры нити носят приближенный характер.

Анализируя формулу (2.100) можно видеть, что высота сечения нити зависит прямо пропорционально от расчетного сопротивления. Предположим, что мы имеет две нити с различными сопротивлениями, но изгибная жесткость первой нити  равна изгибной жесткости второй нити .

Принимая во внимания формулу (2.100), получим отношение 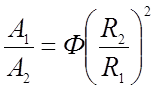, показывающее, что расход металла обратно пропорционален квадрату отношения расчетных сопротивлений.

Оценивая напряженно-деформированное состояние нити, изогнутой по кубической параболе и нити, выполненной из двух прямолинейных стержней можно заметить, что для двухполюсного радиально-вантового покрытия, пролет нитей в котором не превышает 40м, простым решением будет система, жесткие нити, в которой выполнены из двух прямолинейных стержней. С увеличением пролета прогибы и изгибающие моменты в такой нити значительно превосходят прогибы и изгибающие моменты в нити, изогнутой по кубической параболе.

Для того, чтобы их уменьшить, необходимо увеличить изгибную жесткость нити или уменьшить ее начальную стрелку. В том и другом случае это приводит к увеличению расхода металла на нити. Поэтому для покрытий, имеющих пролет более 40м, необходимо ввести в систему изгибно-жесткие элементы, изогнутые по кубической параболе.