Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 2

Это уже значительный момент, который прямо пропорционален j и обратно пропорционален квадрату коэффициента гибкости. Он растет по мере удаления от опоры, достигая максимума в сечении, отвечающему условию

Для трёхшарнирной нити, если отбросить величины бесконечно малы, максимальное значение будет отвечать условию:

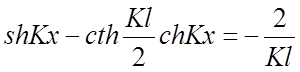                                                                     (2.31)

Обозначим 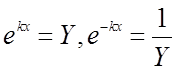  и подставляя в (2.31), получаем:

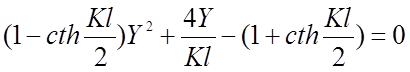                                                     (2.32)

Решая уравнение, определяем Y, а затем находим величину X, т.е. расстояние, где возможен максимум, по формуле:

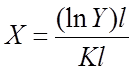                                                                                            (2.33)

Для гибкой нити максимум второй производной находится в центре пролета. С уменьшением Kl (рис.2.4.) максимум смещается к опорам. Величина абсциссы для различных Kl приведена в таблице 2.4.                       

Таблица 2.4.

Kl	4	8	9	10	12	14	16	18	20	¥
X	0.2l	0.173l	0.167l	0.167l	0.149l	0.139l	0.130l	0.122l	0.115l	0

Принимая во внимание, что для реальных нитей cth весьма близко приближается к единице, формула 2.31 для экстремальной точки с некоторым приближением будет иметь вид:

shKx–chKx =-2/Kl.                                                                            (2.34)

Для определения Х получаем формулу:

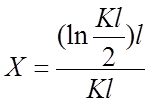.                                                                                         (2.35)

Учитывая выражение (2.34), (2.35) для вычисления максимального момента получаем приближенную формулу, удобную для практического применения

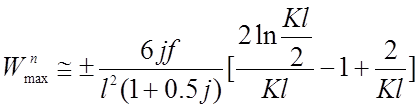                                                   (2.36)

Максимальные изгибающие моменты при половинном загружении пролета временной нагрузкой, определяются по формуле:

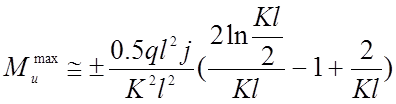                                                       (2.37)

Анализируя работу нитей изогнутых по кубической параболе, замечаем, что фиктивная нагрузка, изгибающая нить, достигает максимального значения в середине пролета равного

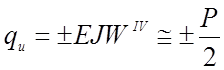                                                                                (2.38)

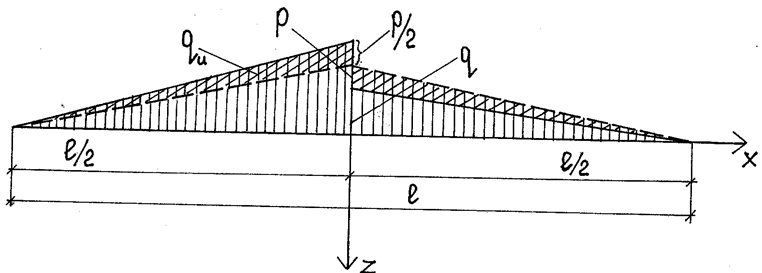
При этом в правом полупролете она добавляется к действующей нагрузке, а в левом полупролете вычитается из нее (рис.2.5.). Из чего можно заключить, что для нити, обладающей изгибной жесткостью, такая нагрузка является локальной и изгибная жесткость стремится перераспределить ее так, чтобы та приблизилась к равновесному состоянию.

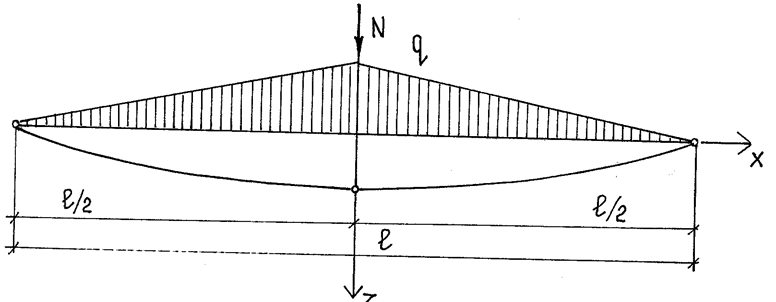
б) Сосредоточенная сила в середине пролета нити.

Рис. 2.8. Расчётная схема нити

Рис.2.9. Расчётная схема нити

Рис.2.10. Расчётная схема нити

Сосредоточенной силой в середине пролета нити может быть световой фонарь, подвешенное оборудование, а также контактная сила, возникающая от диагонального элемента (рис.2.6, 2.7). Используя уравнение 2.4, получаем для трёхшарнирной нити:

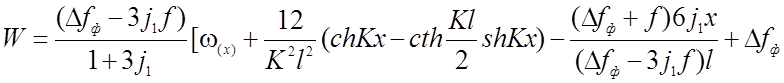      (2.39)

для двух шарнирной нити: 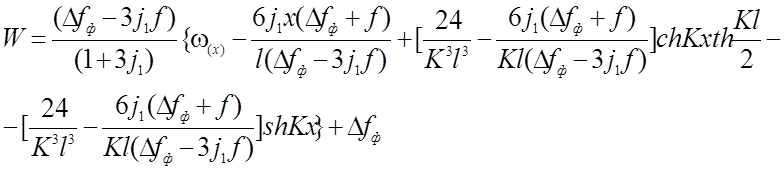                              (2.40)

Здесь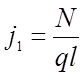

При выводе формул (2.39), (2.40) "балочный" изгибающий момент в середине пролета был принят .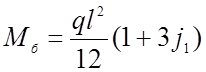

Пренебрегая членом 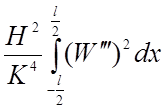 и введя обозначения, принятые при выводе (2.16), получаем разрешающее квадратное уравнение относительно :

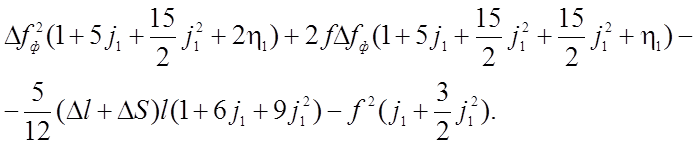            (2.41)

В отличие от (2.16) свободный член в (2.41) содержит кроме коэффициента растяжимости еще и коэффициент j₁, зависящий от центральной силы. Таким образом, в зависимости от коэффициента j₁, прогиб Df_ф может быть значительным даже при нерастяжимой нити. При этом в сечении нити возникают гораздо большие изгибающие моменты. Интересно проследить за второй производной W" в сечении под силой.

Дифференцируя дважды (2.40) и приравнивая нулю, получаем для двух шарнирной нити:

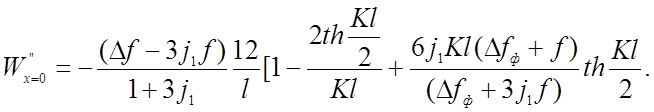                  (2.42)

Из (2.42) видно, что с уменьшением жесткости третий член в скобках неограниченно возрастает. Это говорит о том, что изгибная жесткость необходима в висячих покрытиях, так как ограждает его от недопустимо больших искривлений, вызванных сосредоточенными силами. В трёхшарнирной нити сосредоточенная сила приводит к увеличению стреловидности.

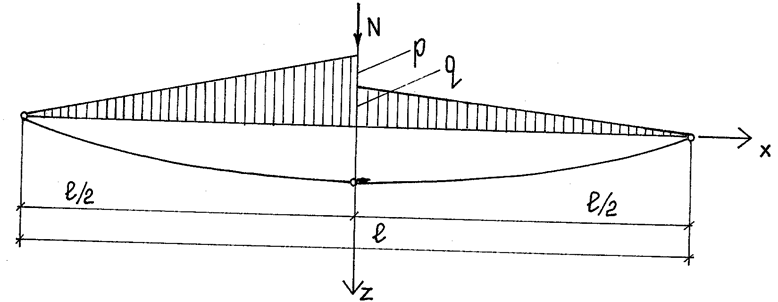
в) В качестве примера рассмотрим более общий случай загружения нити, приложив наряду с нагрузкой g и P сосредоточенные силы N и Ф в центре нити, возникающие в двухполюсном радиально-вантовом покрытии в результате действия диагонального элемента на жесткие нити (рис.2.8).

Уравнения прогибов для трёхшарнирной нити получают вид:

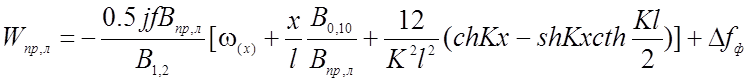     (2.43)

Значения коэффициентов j_1, j, j₂, B_пр, В_л, В₁₀, В_1, В₂ приведены в таблице 2.5.

Для двух шарнирной нити решение дифференциального уравнения дано в таблице 2.5.

Для определения фиктивного прогиба используем формулу (2.10), подставляя соответствующие значения D_r, M_d, h₁, h₂, которые приведены в таблицах (2.1, 2.5).