Анализируя полученные решения, видим, что сила N уменьшает прогибы в загруженной половине и увеличивает их в незагруженной. Сила Ф уменьшает прогибы в обеих половинах, поэтому она является полезной. Полученные формулы являются необходимыми для расчета системы, включающей жесткие нити и диагональный элемент, но не достаточны. Для определения контактной силы Ф необходимо знать горизонтальное перемещение центрального узла нити.
 |
Из рассмотренных примеров нагружения нити, изогнутой по кубической параболе, можно видеть, что влияние жесткости на деформации может быть различно и зависеть от четырех основных причин:
1. От растяжимости, которую можно оценить как способность к удлинению в пределах расчетного сопротивления. Она выражается отношением расчётного сопротивления к модулю упругости. Для стальных нитей, имеющих одинаковый модуль Е растяжимость пропорциональна расчетному сопротивлению стали;
2. От перемещения опор, величина которых зависит от конструкций опор и сооружения в целом и может колебаться в очень широких пределах, в некоторых случаях намного превышая растяжимость. Названные две выше причины больше всего проявляются при действии равновесной нагрузки, вызывающей наибольший распор. При неравновесной нагрузке имеют значение еще два фактора;
3.Длина участка действия неравновесной нагрузки или, что тоже - длина отсутствие равновесной нагрузки. С уменьшением длины участка сдерживающее влияние жесткости будет увеличиваться;
4. Отношение массы неравновесной нагрузки к равновесной. С уменьшением этого отношения параметр Kl будет уменьшаться, что повышает влияние жесткости. Тоже самое можно констатировать, если мы будем увеличивать начальную стрелку f.
3. ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНЫХ ПЕРЕМЕЩЕНИЙ
В ЖЕСТКОЙ НИТИ.
Горизонтальные перемещения DХ любой точки нити, находящейся на расстоянии Х от опоры, определим как разность между начальной и конечной длиной на участке Х (рис.2.9). Если нить при таком перемещении растянулась или сжалась в пределах этой длины на DSx , то это должно учитываться так же, как и угол j наклона нити к горизонту.
В общем случае их вычисляют из выражения
И=(Sx-Sxi+DSx)cosj , (2.44)
где Sx - длина участка нити в исходном состоянии;
Sxi - то же, после перемещения, вызванного новым нагружением.
Таким образом, сначала определяют новое положение данной точки, а потом ее перемещение.
Рассмотрим определение горизонтальных перемещений нити в двухполюсной системе, загруженной несимметричной нагрузкой. Для упрощения расчета и исследования, так же как и при определении вертикальных перемещений, сначала будем рассматривать нить не связано с системой.
Полагая для пологих нитей cos j(х) равным единице, получаем для определения горизонтальных перемещений в сечениях выражение:
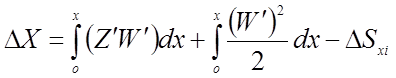, где
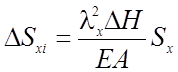(2.45)
Определим горизонтальное перемещение для нити (рис.2.4), начальное очертание у которой принято по кубической параболе.
Определив производные, вычислив интегралы и произведя все преобразование, получим в середине пролета для пологой жесткой нити горизонтальное перемещение:
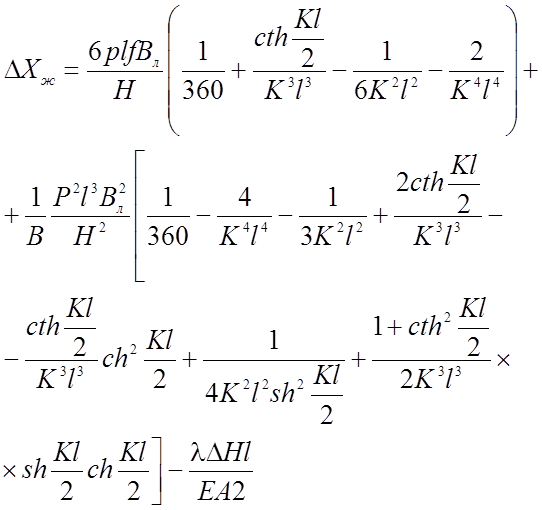(2.46)
Для гибкой нити имеем:
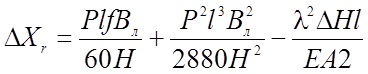(2.47)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.