Оценка стабилизации висячего покрытия не может быть одинаковой на все случаи его конструктивных решений. В зависимости от применения типа ограждающих конструкций, материала обшивки, усилий преднапряжения, а также требований эксплуатации - задачи стабилизации могут быть различны. Следует заметить, что висячее покрытие должно быть стабилизировано не только вдоль, но и поперек пролета, поэтому необходимо ограничивать изменение кривизны также предельной величиной.
Если кровельное покрытие - настил или плита скреплены с нитью по всей длине, то они образуют общую конструкцию, деформации которой будут совместны. При этом деформации настила Е будут суммироваться из деформаций от относительного удлинения и от искривления оси Е=Е0+Eи.
В зависимости от материала неблагоприятной может быть не только величина искривления W", но и ее знак. Так, например, для железобетонной плиты может оказаться невыгодным не увеличение, а уменьшение кривизны, которое вызывается местным нагружением не на данном участке, а какого-либо отдаленного от него.
Решение задачи усложняется тем, что для составного сечения, в которое входит нить и ограждающееся конструкция, каждый слой может соединятся между собой податливыми связями.
Тогда суммарные напряжения в настиле (ограждающих конструкции) могут быть определены из выражения:
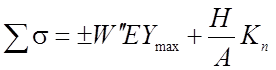(2.51)
где Е - модуль упругости настила,
Ymax - расстояние от нейтральной оси до наиболее удаленного волокна,
W" - изменение кривизны под нагрузкой,
Н - усилие растяжения,
А - площадь обшивки,
Кп - коэффициент учитывающий податливость связей.
Численное значение коэффициента Кп определяется при совместном решении дифференциального уравнения жесткой нити и уравнений составного стержня.
Путем снижения или увеличения жесткости связей можно регулировать напряжение в обшивке, причем, чем большей прочностью обладает обшивка, тем более жесткими связями могут крепиться к жестким нитям ограждающие конструкции, что выгодно для стабилизации, т.к. приведенная жесткость возрастает, и, наоборот, с уменьшением напряжений в настиле нужно снижать жесткость связей. Предлагаемая методика оценки напряженно-деформированного состояния позволяет определить напряжение не только в несущих, но и в ограждающих конструкциях, а также деформированные способности покрытия в целом.
Общая рекомендация по применению настила заключается в том, чтобы его эластичность и определяемые его допустимые искривления во всех направлениях превосходили возможные искривления несущей конструкции. При этом допустимое искривление для кровельного настила может колебаться в широких пределах в зависимости от выбранного материала, толщины и слитности слоев, композиционных особенностей и т.д. .
Определение максимальных искривлении нити в зависимости от величины местной нагрузки и изгибной жесткости покажем на примере трехшарнирной нити, изогнутой по кубической параболе. Для решения поставленной задачи воспользуемся уравнением (2.4).
Для нити, изображенной на рис.2.11, общее решение дифференциального уравнения имеет вид:
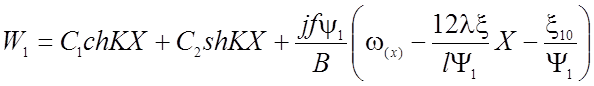
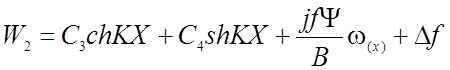(2.52)
Постоянные интегрирования определяются из граничных условий:
при X = 0 W2=Df , при X = a W1=W2 ,
при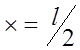 
W1=0 , при X =
a W'1=W'2 .
Подставляя постоянные интегрирования в уравнение (2.52), получаем для прогибов выражения:
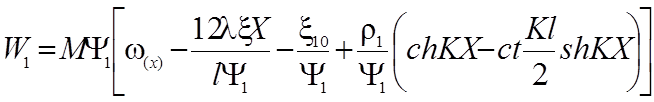
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.