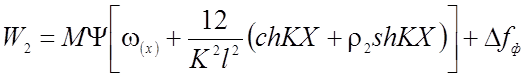Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 3

,                                   (2.53)

где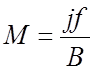

       

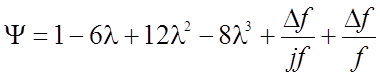
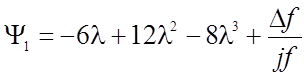
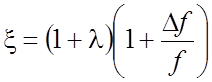
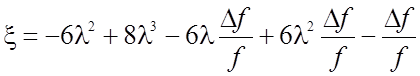
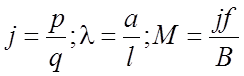
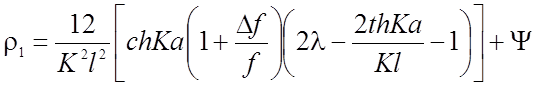
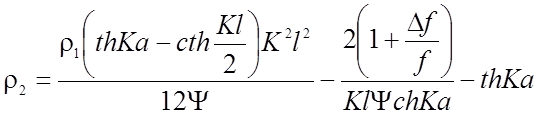
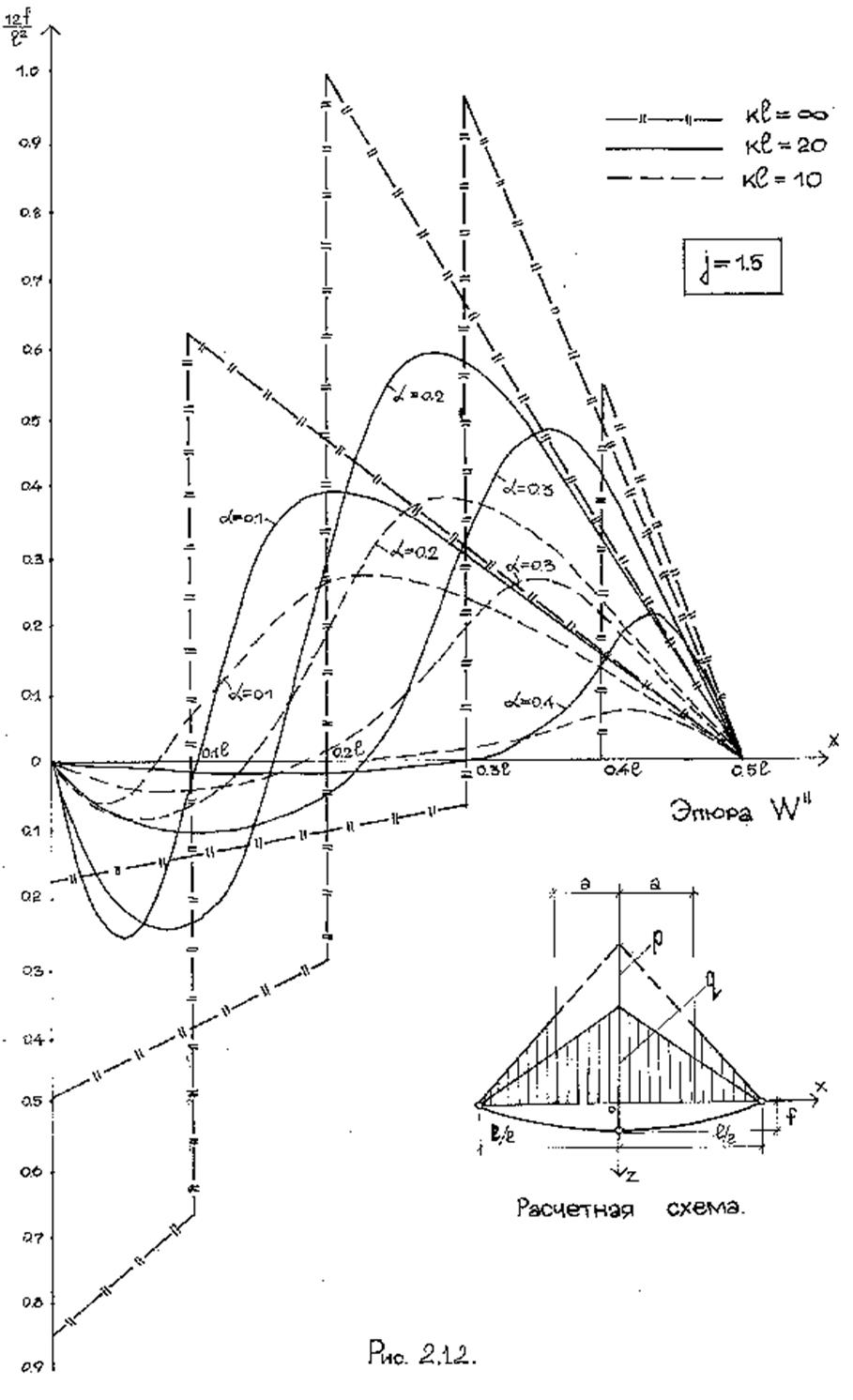
Для нити, приведенной на (рис.2.12) формулы (2.53) остаются без изменения, но коэффициент 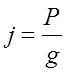  во всех выражениях необходимо заменить на  

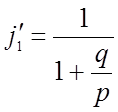
Продифференцировав дважды уравнение (2.53) получим выражения для искривлений при заданной нагрузке:

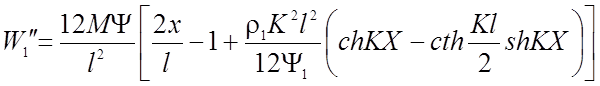                          (2.54)

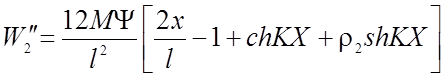                                                (2.55)

Величина распора H определяется из уравнения (2.11)

Для определения максимального искривления в нити при заданной нагрузке вычислим третью производную от прогиба и приравняем ее нулю. Для первого и второго участков, соответственно имеем

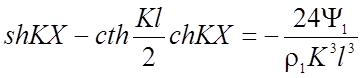                                                            (2.56)

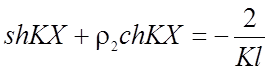                                                                         (2.57)

 Обозначим ,  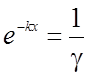и подставим в (2.46) и (2.47), получим

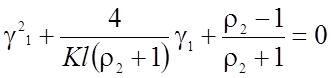                                                                (2.58)

Величина Х, т.е. расстояние, где возможен максимум определяется по формуле (2.23). Подставляя полученные значение в формулы, находим величину максимального искривления.

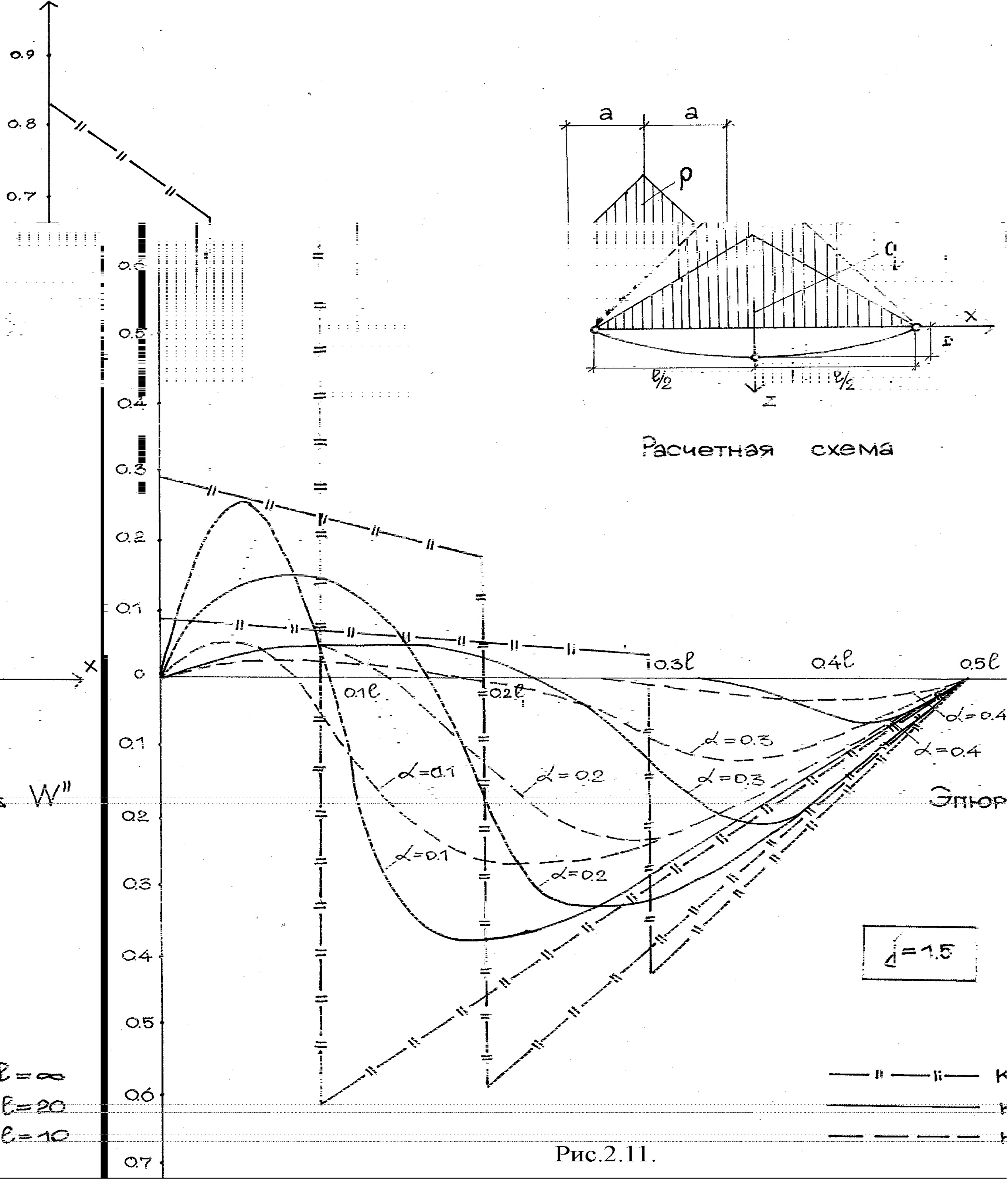
В качестве примера были вычислены искривления двухполюсного покрытия, для которого равновесной нагрузкой является треугольная возрастающая к середине пролета. Временная местная нагрузка Р принималась равной 1,5q. Участок загружения принимался в пределах от 0,1l до 0,9l через 0,9l. Результаты вычисления (рис.2.11 и 2.12) показывают, что изменение кривизны имеет два максимума - один на загруженном, другой на незагруженном участке. Интересно отметить, что наибольший по абсолютной величине максимум оказался отрицательным. Он появился примерно в четверти пролета на незагруженном участке. Даже сравнительно набольшая жесткость нити заметно уменьшает искривление. Так при kl = 10 искривления составляют 38% от искривления гибкого покрытия. Сравнивая график искривлений от загружения половины пролета, видим, что загружение местной нагрузкой может привести к большим искривлениям и быть в этом смысле более опасным.

Анализируя эпюры W^" , приведенные на (рис. 2.11 и 2.12) можно сделать следующие выводы:

1. По мере увеличения интенсивности равновесного нагружения нити стабильность ее растет, склонность к искривлению от добавочной нагрузки уменьшается.

2. Чем меньше длина загружения нити, тем сильнее влияние изгибной жесткости, которая как бы распределяет нагрузку на участок большей длины, чем участок загружения. Следовательно, введение изгибно - жестких элементов эффективно прежде всего для уменьшения искривлений от локальных нагрузок, позволяет снизить существенно распор, что приводит к уменьшению расхода материала на нить, анкерные устройства и опорный контур.

3. Искривление нити обратно пропорционально действующему распору, поэтому уменьшение минимального распора ниже определенно для данной кровли при данной жесткости недопустимо.

5. Выбор рациональных параметров нити.

В предыдущем параграфе мы рассмотрели как ведет себя нить под различными нагружениями и как меняется влияние жёсткости в зависимости от вида и массы нагрузки. Вследствие этого можно ответить на вопрос - как назначить по возможности наиболее рациональные параметры, создающее наилучшее напряженно-деформированное состояние нити при всех возможных комбинациях нагрузки.

Надо сказать, что такой вопрос не может быть решен узко только для нити, являющейся частным элементом всего сооружения. Параметры нити должны быть подчинены лучшему решению всего покрытия в целом, включая и опорный контур. Однако, по-видимому, задача нахождения рациональных параметров здания в целом включает в себя и нахождение рациональных параметров нити.

В этом направлении проведены большие теоретические и экспериментальные исследования Н.С.Москалевым. Применяя его методику, разработанную для нити, очерченной по квадратной параболе, найдём рациональные параметры для нити, выполненной по кубической параболе.

Основными параметрами нити являются пролет, стрелка, расчётное сопротивление R, модуль упругости Е, изгибная жесткость EI, площадь сечения А, высота сечения нити h. Пролет нити и стрелка f будем считать известными величинами, так как на их выбор оказывают влияния требования технологии, эксплуатации, а также требования, предъявляемые к архитектурной выразительности здания. Остальные параметры могут быть назначены, исходя из рациональных условий работы нити.

При загружении в нити возникают напряжения от осевого растяжения и изгиба. При этом нами было установлено, что при равновесной нагрузке преобладают осевые напряжения, при неравновесной нагрузке происходит увеличение краевых напряжений изгиба. В первом случае осевые напряжения меняются обратно пропорционально стрелки f. Краевые напряжения от изгиба находятся в прямой пропорциональной зависимости от стрелки. Результирующее напряжение, равное s = s_р + s_и, зависит от материала, способов и последовательности образования жесткости и наличия предварительного напряжения, поэтому напряжение в крайних волокнах возможно регулировать в нужном направлении.