Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 3, страница 3

Если высота сечения нити подобрана по формуле (2.67), то напряжения, возникающие от изгиба, можно определить приближенно по формуле:

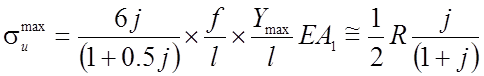                                          (2.68)

где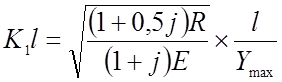   

( при выводе J º А´Y²_max)

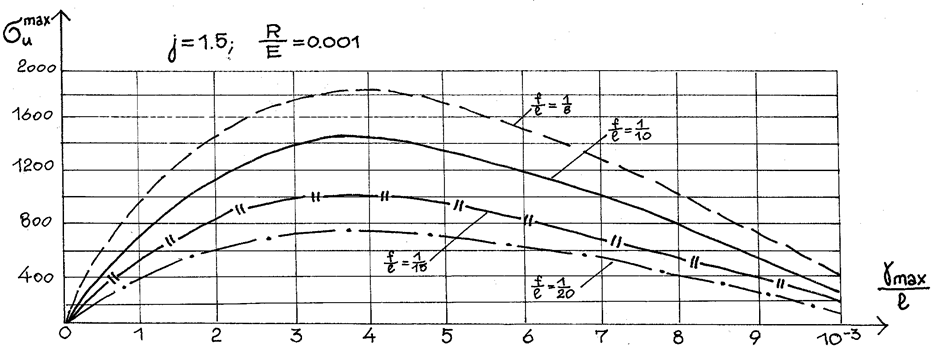
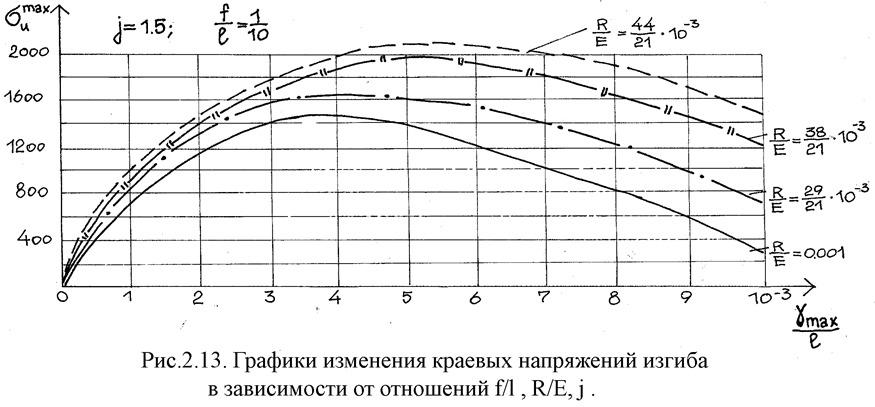
Рассматривая полученные формулы, видно, что при постоянном моменте инерции рост высоты сечения сопровождается ростом краевых напряжений изгиба. Причем эта зависимость носит прямо пропорциональный характер. Чтобы ограничить рост краевых напряжений величиной расчетного сопротивление необходимо уменьшить стрелку или увеличить расчётное сопротивление. Однако, возможен другой вариант, когда рост высоты сечения сопровождается увеличением момента инерции при сохранении неизменной площади. В этом случае краевые изгибные напряжения будут сначала расти (рис.2.13), при больших значениях Kl, но затем, достигнув максимума, начнут падать, при дальнейшем росте высоты сечения, благодаря возрастающему влиянию жесткости.

Для того, чтобы правильно назначить сечение жесткой нити, недостаточно знать только высоту сечения. Требуемую площадь сечения определяем исходя из загружения нити полной расчетной нагрузкой, включающею постоянную и временную снеговую нагрузку на покрытие. При этом заметим, что максимальное тяжение возникает вблизи опор, т.е. там, где напряжение от изгиба, которые и так незначительны при равновесном загружении, равны нулю.

Поэтому для практических расчетов при назначении А_тр можно пользоваться формулой:

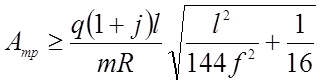                                                                  (2.69)

где m - коэффициент условия работы.

Требуемую изгибную жесткость подбираем по заданному прогибу от загружения нити временной нагрузкой Р в одном полупролете. Используя (2.19) и обозначая допускаемый прогиб через W получаем:

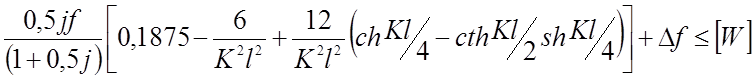      (2.70)

Решая данное уравнение методом последовательных приближений, определяем Kl, затем находим требуемый момент инерции по формуле:

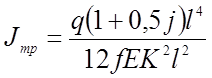                                                                                           (2.71)

Наряду с предложенным методом возможен другой. Принимая за основу Формулы (2.18; 2.19 и 2.69), определяем в параметрическом виде величину относительно прогиба:

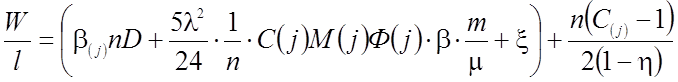               (2.72)

Здесь ;    ;   ;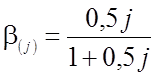

              

        

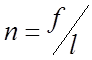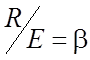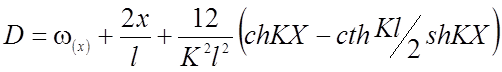
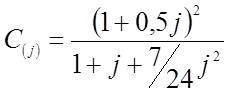
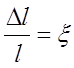
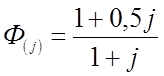
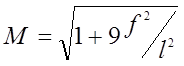
m - коэффициент условия работы.

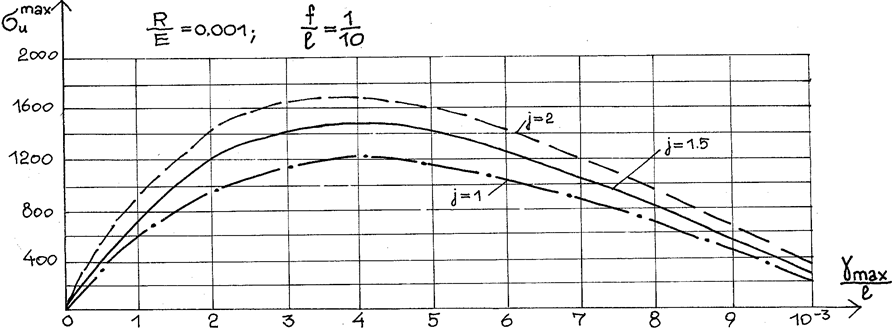
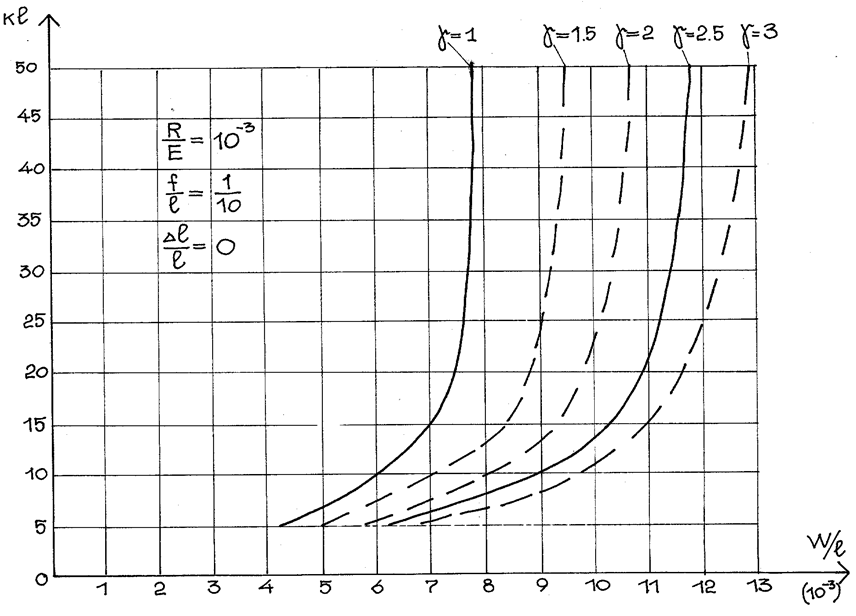
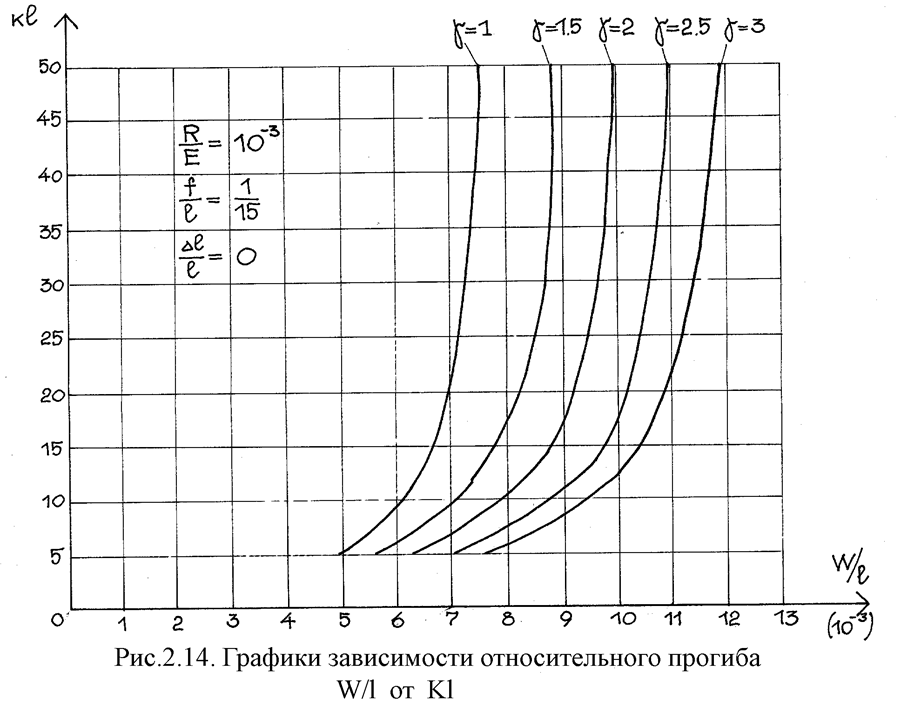
Зная величину абсциссы, при которой прогиб достигает максимального значения (табл.2.3), определяем относительный прогиб в зависимости от параметров Kl, , , 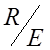, j. Полученные зависимости приведены на рис. 2.14. Теперь, если известна величина зависимости допускаемого прогиба, графически можно определить значение Kl при заданных параметрах и по формуле (2.71) вычислить момент инерции.

Требуемый момент инерции необходимо определить также в зависимости от допускаемого искривления, которое определяется типом кровли. Используя выражение (2.20) данное условие запишется так:

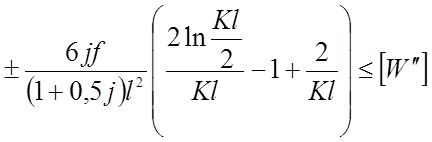                                                  (2.73)

Величина абсциссы, при которой W достигает максимума определяется по формуле (2.25), ее значение для различных Kl приведены в таблице (2.4). В первом приближении можно принять X = 0.16l, затем полученный результат уточнить. Тогда для определения Kl получим выражение:

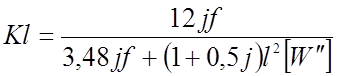                                                               (2.74)