Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 3, страница 5

                                                                              (2.77)

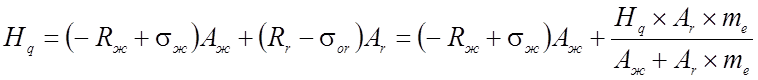   (2.78)

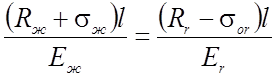                                                                                  (2.79)

Физический смысл первого уравнения: усилие предварительного напряжения в гибкой нити уравновешивает сжимающие усилие предварительного напряжения в жесткой нити. По уравнению (2.77) нагрузка, приложенная после предварительного напряжения, уравновешивается приращением усилий в гибкой и жесткой нити.

Из уравнения (2.78) следует, что величина приращения усилия в гибкой нити от нагрузки, приложенной после предварительного напряжения, пропорциональна отношению площадей гибкой нити и всего элемента с поправкой на отношение модулей упругости материала гибкой и жесткой нитей. Уравнение (2.79) выражает равенство удлинений гибкой и жесткой нитей от действия нагрузки.

Жесткая нить на 1 этапе воспринимает сжимающие усилие. При этом может потерять устойчивость, если ее размеры не обеспечат необходимую жесткость или не будут приняты специальные меры. Возможна и потеря местной устойчивости стенки в сжатой зоне. Поэтому устойчивость стенки надо проверять расчетом и при необходимости укреплять ребрами. Общая устойчивость жесткой нити в плоскости покрытия обеспечивается укреплением ее примыкающими элементами: настилом и балками, которые связаны с растянутыми элементами.

Решая совместно уравнения (2.76 - 2.79), получаем формулы для определения требуемой площади сечения жесткой и гибкой нити:

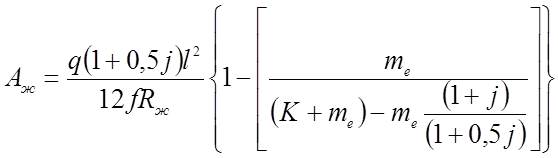                                (2.80)

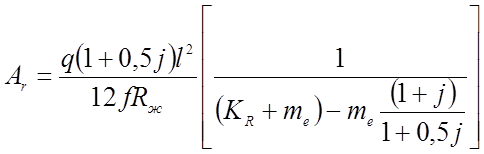                                          (2.81)

Требуемый момент инерции исходя из заданного прогиба и допускаемого искривления определяется из выражений (2.70 и 2.74). При этом считаем, что вся изгибная жесткость сосредоточена в жесткой нити.

Так как предварительно усилие в гибких нитях подобрано с учетом того, что при неравновесном загружении в жесткой нити не возникает продольных сил, то вместо (2.67) становится возможным условие

                                                                                 (2.82)

Сравнивая формулы (2.67 и 2.82) замечаем, что предварительное напряжение жесткой нити позволяет значительно увеличить ее высоту и добиться стабилизации. С ростом Y_max будет падать А₁, что в свою очередь расширяет возможности для сталей высокой прочности.

6. Исследование работы жестких нитей, выполненных из двух прямолинейных элементов.

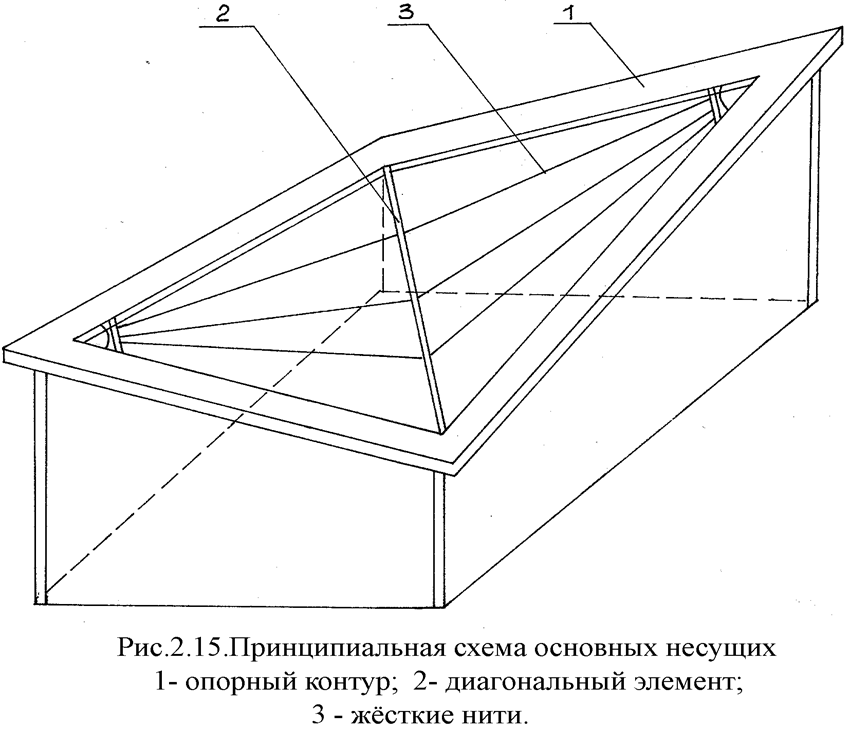
С целью повышения производительности труда при изготовлении, снижения трудоемкости и сроков монтажа, которые определяют стоимость конструкции, предлагается в двухполюсном покрытии заменить жесткие нити, изогнутые по кубической параболе, нитями, выполненными из двух прямолинейных элементов (рис.2.15, 2.16 ).

Целесообразность применения таких нитей в рассматриваемой системе объясняется, во-первых, тем, что для полной расчетной нагрузки, большая часть которой сосредоточена в центре пролета нитей, равновесное очертание  описывается кубической параболой, которая имеет вблизи опор прямолинейных участок большой протяженности. Во-вторых, вертикальные и горизонтальные сосредоточенные силы, возникающие в результате взаимодействия диагонального элемента с жесткими нитями, как будет показано ниже, существенно уменьшают прогибы и моменты.   

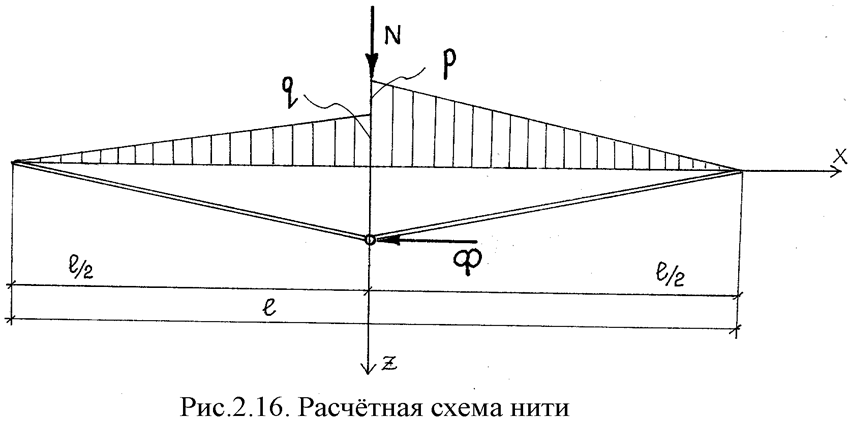
Используя формулы и допущения, принятые при расчете жестких нитей, изогнутых по кубической параболе, выполним расчет жестких нитей из прямолинейных элементов, первоначально считая их несвязанными с системой.

В общем случае загружения нить воспринимает постоянную нагрузку q, временную нагрузку Р, расположенную на половине пролета и сосредоточенные силы F и N (рис.2.16).