Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 3, страница 2

При этом, желательно, чтобы рост одних напряжений сопровождался бы уменьшением других, а суммарные напряжения в верхних фибровых волокнах при различных видах загружения были бы примерно равны и приближались к расчетному сопротивлению. Если при полной расчетной нагрузке очертание нити принимаем равновесным, то напряжения s_р будут максимальными. При неравновесной нагрузке осевое растяжение значительно уменьшится, а возрастающие при этом краевые напряжения можно будет воспринять за счет этого уменьшения.

Рассмотрим нить, изогнутую по кубической параболе с шарниром в центре. Условие равнопрочности нити при равновесном загружении и при загружении неравновесной нагрузкой приводит к равенству краевых напряжений в том и другом случаях нагрузки:

s = s _р^п  + s_и^п  = s_р^0,5 + s_и £ R                                                              (2.59)

где   ;           ;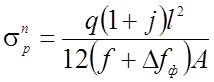

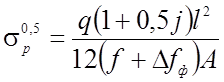s_и = ± W"ЕU_max - краевые напряжения от изгиба,

U_max - расстояние от нейтральной оси до наиболее удаленной точки  сечения.

При равновесной нагрузке максимальные фибровые напряжения определяются по формуле:

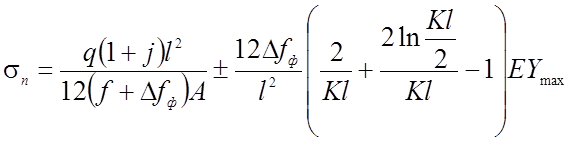                              (2.60)

Для неравновесной нагрузки, учитывая (2.26), напряжения определяются по формуле:

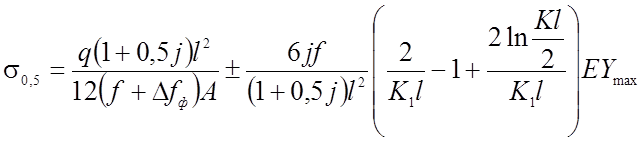                    (2.61)

Теперь для того, чтобы определить рациональное значение стрелки, высоту сечения или отношения стрелки к пролету сравним напряженное состояние из условия полного равновесного загружения с нагружением полупролета временной нагрузкой. Вычитая (2.61) из (2.60) и преобразовывая разность, получаем кубическое уравнение относительно стрелки:

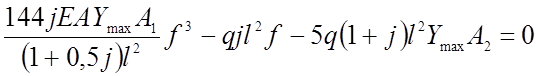                                   (2.62)

где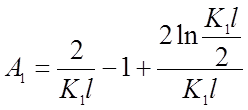       

     

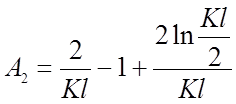
При выводе (2.60) мы принимали Df_ф, вычисленное по формуле (2.11), и f+Df_ф=f .

В формулу входит величина А, которая зависит от пролета, стрелки и нагрузки. Однако, приближенно ее можно определить из выражения:

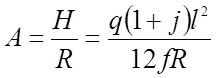                                                                                 (2.63)

Подставляя (2.63) в формулу (2.62), получаем квадратное уравнение:

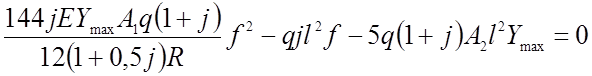                           (2.64)

Анализируя полученную формулу, замечаем, что ее можно упростить, так как изгибающие моменты, возникающие в жесткой нити от равновесного загружения, малы.

Подставляя в выражение (2.60) значение Df_ф и А, выразим напряжения изгиба через расчетное сопротивление.

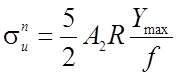                                                                                      (2.65)

Формула (2.65) показывает, если нить имеет высоту сечения, небольшую по сравнению со стрелкой, то свободный член в уравнение (2.64) можно опустить и оно сведется к виду:

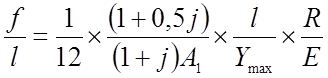                                                                 (2.66)

Или, решая относительно Y_max, получим:

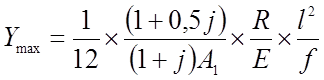                                                                 (2.67)

Из выражения (2.67) видно, что высота сечения нити зависит от отношения временной нагрузки к постоянной, от параметра Kl, от отношения стрелки к пролету и от отношения расчетного сопротивления к модулю упругости. Таким образом, высота сечения нити не может быть любой, а должна соответствовать условию (2.67). С повышением расчетного сопротивления стали увеличиваться высота сечения. А это значит, что появляется возможность достичь требуемой жесткости не за счет увеличения площади сечения нити, а за счет увеличения высоты сечения. Таким образом, применение в жестких нитях сталей высокой прочности приводит, во-первых, к снижению площади сечения, во-вторых, к увеличению жесткости покрытия за счет роста высоты сечения.