При загружении нити неравновесной нагрузкой происходит более резкое изменение начальной формы нити, чем при полной, так как эта нагрузка заставляет нить принять форму подобную эпюре моментов, что влечет за собой рост изгибающих моментов и напряжений от изгиба. Влияние изгибной жесткости на работу нити для такой нагрузки становится более существенным. Рассмотрим в качестве примеров 3 случая действия неравновесной нагрузки на нить, имеющей в исходном состоянии очертание кубической параболы.
a) Постоянная нагрузка q расположена на всем пролете, временная нагрузка р - на одной половине пролета.
Постоянные интегрирования для нити (рис. 2.2.в) находим из следующих условий.
при 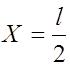
![]()
при
X=0 ![]()
Решая уравнение (2.4) и подставляя значение постоянных коэффициентов, получаем для нити, имеющий в центре шарнир, решение в виде
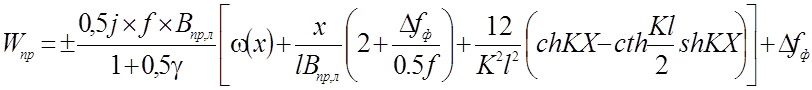 (2.24)
(2.24)
Здесь 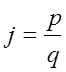 ;
; 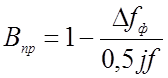 ;
;
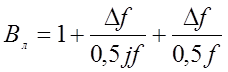
Для нити (рис.2.2.г) постоянные интегрирования находятся из условий:
при 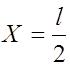 Wл = Wпр =
0
Wл = Wпр =
0
при X=0 W'л = W'пр ; Wл = Wпр
Формула прогибов получает вид:
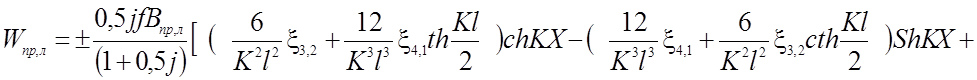
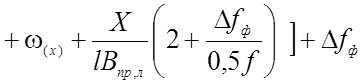 (2.25)
(2.25)
Здесь
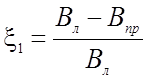
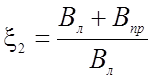
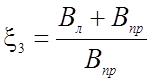
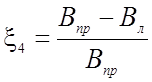
Прогиб Dfф определяется по методике изложенной
выше. Подставляя в (1.9) h1 и h2 и Dr , значение которых приведены в таблицах (2.1, 2.2) и
пренебрегая членом 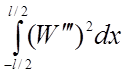 получим разрешающее квадратное
уравнение относительно Dfф
получим разрешающее квадратное
уравнение относительно Dfф
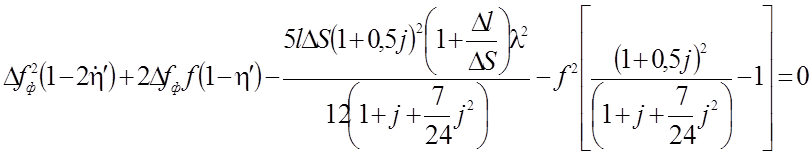 (2.26)
(2.26)
Для практических вычислений с достаточной степенью точности можно пользоваться приближенной формулой:
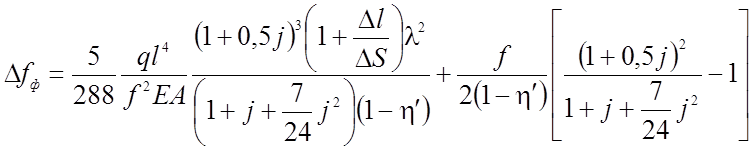 (2.27)
(2.27)
Рассматривая полученные решения, необходимо подчеркнуть, что фиктивный прогиб в середине пролета нити при неравновесном загружении значительно меньше, чем при полном и зависит от отношения временной нагрузки к постоянной даже при нерастяжимой нити не стремится к нулю.
Анализируя формулы (2.24,
2.25) и эпюры W (рис.2.4) видим, что в зависимости от отношения ![]() и стрелки f, прогибы могут быть
весьма большими и во много раз превосходит прогибы от равновесной нагрузки.
Существенное влияние на работу нити оказывает изгибная жесткость, которая
сдерживает перемещения нити.
и стрелки f, прогибы могут быть
весьма большими и во много раз превосходит прогибы от равновесной нагрузки.
Существенное влияние на работу нити оказывает изгибная жесткость, которая
сдерживает перемещения нити.
Для определения места максимального прогиба вычислим первую производную от прогиба и приравняем ее к нулю. Приближенно абсцисса максимума для нити на (рис.2.2а) определяется из выражения:
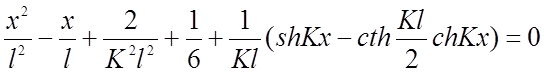 (2.28)
(2.28)
Для различных значений Kl в таблице 2.3 и на (рис.2.4) приводятся значения абсцисс, при которых прогиб достигает максимума.
Таблица 2.3.
|
Кl |
4 |
8 |
12 |
16 |
20 |
¥ |
|
X |
0.24l |
0.235l |
0.226l |
0.223l |
0.2195l |
0.2114l |
Из таблицы видно, что с увеличением Kl максимум прогиба смещается к центру. Для нитей, обладающих изгибной жесткостью, применяемых в висячих покрытиях с некоторым приближением можно считать, что максимальное значение прогиба находится в четверти пролета. Тогда его значение можно вычислить по формуле:
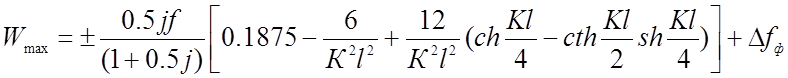 (2.29)
(2.29)
Анализируя влияние жесткости на прогиб нити (рис.2.4.) замечаем, что при Кl=8, кинематическая часть прогиба уменьшается примерно в два раза против прогиба гибкой нити.
Изгибающие моменты определяются из выражения:
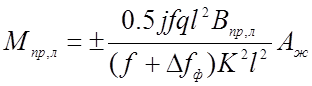 (2.30)
(2.30)
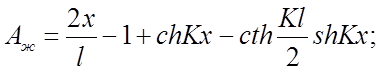

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.