Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 1, страница 2

 S + DS =  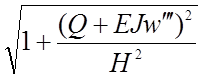     dx                                                (2.5)

Для пологих нитей уравнение (2.5) можно решить относительно распора таким образом:

H = 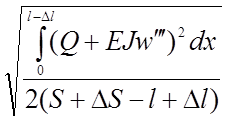                                                                      (2.6)

В первом приближении распор можно вычислить как для гибкой нити, считая, что EJ = 0. Затем, получив решение относительно прогибов w, поставить значение   в выражение (2.6) и скорректировать распор. Если относительная погрешность окажется велика, то расчет необходимо повторить, подставив в формулу (2.4) распор, найденный из выражения (2.6). Разделив равенство (2.4) на EJ и обозначив H/EJ = k², получим уравнение в виде, удобном для решения

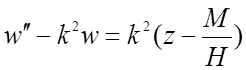                                                                             (2.7)

Решение не представляет затруднений, если коэффициент гибкости k принять постоянным по всей длине. Если же он меняется, то в элементарных функциях решение получить невозможно.

Как будет показано ниже, жесткость, требуемая для нити покрытия, мала и незначительно влияет на распор. Еще меньше будет влиять переменность жесткости, если она происходит вследствие искривления стержня постоянного сечения. Поэтому в дальнейшем изложении при выводе рабочих формул будем считать коэффициент постоянным.

В правой части уравнения (2.7) член M/H представляет собой ординату оси тяжения z_ф, т. е. геометрического места точек, через которые проходит равнодействующая усилий. У гибкой нити, очевидно, кривая тяжения будет всегда совпадать с осью нити. У жесткой нити такого совпадения не будет. Кривая тяжения будет идти выше  или ниже оси, иногда пересекая ось. Она всегда будет проходить через центры шарниров - опорных или в пролете, если нить будет иметь такие шарниры . Из этого  как следствие вытекает , что чем больше шарниров будет иметь жесткая нить, тем меньше при прочих равных условиях будет отклонятся кривая тяжения оси, тем меньше будут моменты, изгибающие нить. Пользуясь понятием кривой тяжения, с жесткой нитью можно обращаться как с гибкой, ось которой совпадает с кривой тяжения.

Итак, ординаты кривой тяжения находят из формулы

z_ф = z + w_ф= M/H

Тангенс угла наклона кривой определяют из равенства :

tg_ф = z'_ф = z' + w'_ф = Q/H     

Вторая производная ординаты кривой тяжения будет

z"_ф = z" + w"_ф = q/H ,

где w_ф, w'_ф, w"_ф - прогибы кривой тяжения и его производные, отсчитываемые от исходной ординаты z, т.е. от того состояния, при котором нить получила жесткость и при котором кривая тяжения еще совпадала с осью.

Из формулы (2.7) можно найти значение прогиба w_ф и его производных:

;

;

;

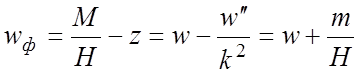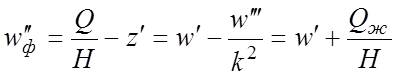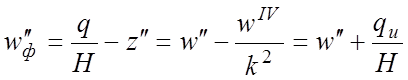где q_и = - EJw^IV - интенсивность реакции жесткой нити на воздействие внешней нагрузки.

Учитывая выведенные соотношения, вместо формулы (2.7) можно записать

w" -  k²w = - k²w_ф                                                                                                                   (2.8)

Общее решение выражение (2.7) получим в виде

w = C₁ ch k x + C₂ sh k x + w*                                                              (2.9) 

где w* - частое решение неоднородного уравнения. Его выражение зависит от правой части ; C₁ и C₂ - постоянные интегрирования, значение которых находят из граничных условий .

Для нахождения прогиба стрелки кривой тяжения Df_ф используем формулу (2.6). Возведя в квадрат и умножив на знаменатель дроби, приводим ее к виду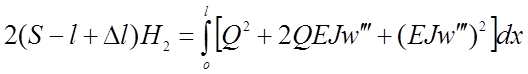

Введя обозначения

  ;                    ;

  ;              ;           ;

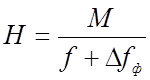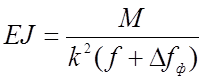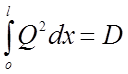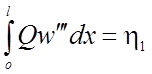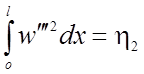деля на D и умножая на ( f + Df_ф )² , получим

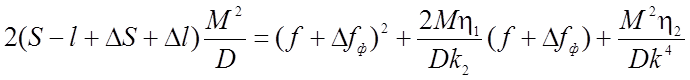             (2.10)