так как гибкость 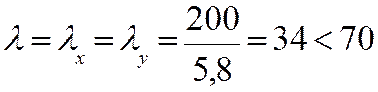 , то коэффициент
продольного изгиба определяем по формуле 20.8
, то коэффициент
продольного изгиба определяем по формуле 20.8
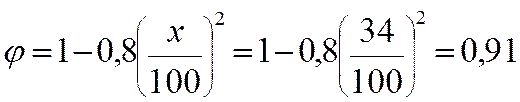
3. Определяем площадь ослабления (рис.20.16)
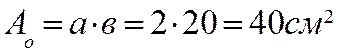 т.к.
т.к. 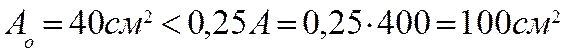 , то за расчетную площадь принимаем
, то за расчетную площадь принимаем 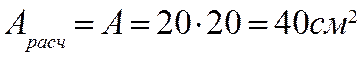
4. Проверяем устойчивость стержня
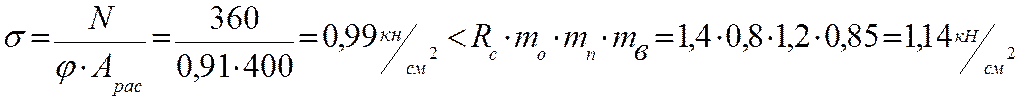 Расчетное
сопротивление сосны на сжатие
Расчетное
сопротивление сосны на сжатие 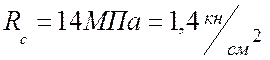 принимаем по таблице
20.2. Коэффициенты, учитывающие условия работы:
принимаем по таблице
20.2. Коэффициенты, учитывающие условия работы: ![]() =0,8 учитывает наличие ослабления;
=0,8 учитывает наличие ослабления; ![]() =1,2 – учитывает то, что стержень
выполняется из древесины лиственницы сибирской (табл.20.3);
=1,2 – учитывает то, что стержень
выполняется из древесины лиственницы сибирской (табл.20.3); ![]() =0,85 (табл.20.4) учитывает температурно
– влажностные условия В3 (табл.20.1).
=0,85 (табл.20.4) учитывает температурно
– влажностные условия В3 (табл.20.1).
Вывод: Напряжение при расчете на устойчивость меньше расчетного сопротивления древесины сжатию, следовательно, несущая способность обеспечена.
Изгибаемые элементы.
Изгибаемые элементы (балки, настилы, обрешетка, прогоны и т.д.) рассчитываются по двум группам предельных состояний. Экспериментальные данные свидетельствуют об упругом характере работы древесины при изгибе, поэтому расчет на прочность по нормальным напряжениям проверяются по формуле (21.10):
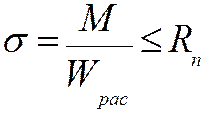 , (21.10)
, (21.10)
где М – изгибающий момент от расчетных нагрузок (кН*см);
![]() -
момент сопротивления рассматриваемого сечения
-
момент сопротивления рассматриваемого сечения 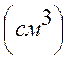 ;
;
![]() -
расчетное сопротивление древесины изгибу
-
расчетное сопротивление древесины изгибу 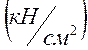 ;
;
момент сопротивления для цельных
деревянных элементов определяют ![]() =
= 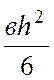 . (рис. 21.5)
. (рис. 21.5)
Расчет прочности по касательным напряжениям в зонах действия наибольших поперечных сил (возле опор) проверяется по формуле (21.11):
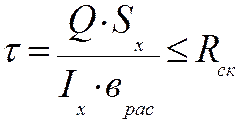 , (21.11)
, (21.11)
где Q – расчетная поперечная сила, (кН);
![]() -
статический момент сечения элемента (см
-
статический момент сечения элемента (см![]() ),
), 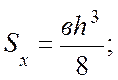
![]() - момент
инерции сечения элемента (см
- момент
инерции сечения элемента (см![]() ),
), 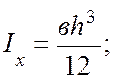
в![]() - расчетная ширина сечения элемента
(см);
- расчетная ширина сечения элемента
(см);
![]() -
расчетное сопротивление древесины скалыванию вдоль волокон при изгибе определяется
по табл.20.2
-
расчетное сопротивление древесины скалыванию вдоль волокон при изгибе определяется
по табл.20.2 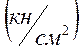 .
.
Расчет по предельным состояниям второй группы, осуществляют как проверку величины прогиба изгибаемого элемента от нормативных нагрузок.
Расчет выполняется по формуле (21.12):
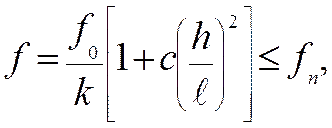 (21.12)
(21.12)
где ![]() -
прогиб балки постоянного сечения (см);
-
прогиб балки постоянного сечения (см);
h – наибольшая высота сечения (см) см. рис. 20.18;
![]() -
пролет балки (см);
-
пролет балки (см);
к – коэффициент, учитывающий влияние переменности высоты сечения, принимается равным 1 для балок постоянного сечения;
с – коэффициент, учитывающий влияние деформаций сдвига от поперечной силы.
Значение коэффициентов к и с для основных расчетных схем балок принимается по (табл.3, приложения 4 СНиП II-25-80).
![]() -
предельный прогиб для изгибаемого элемента (см) см. (5.).
-
предельный прогиб для изгибаемого элемента (см) см. (5.).
значение прогиба ![]() определяется по правилам сопротивления
материалов см.прил. табл.
определяется по правилам сопротивления
материалов см.прил. табл.
Пример21.3 подобрать сечение однопролетной
шарнирно опертой балки (рис.21.19), древесина сосна 2-го сорта. Балка имеет
пролет ![]() = 4м и воспринимает равномерно –
распределенные нагрузки нормативную
= 4м и воспринимает равномерно –
распределенные нагрузки нормативную 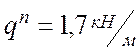 , и расчетную
, и расчетную 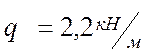 . Балка устанавливается в отапливаемом
помещении.
. Балка устанавливается в отапливаемом
помещении.
Решение:
1. Подбираем сечение балки из условия
прочности. Максимальный изгибающий момент 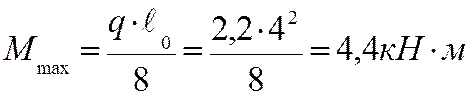 =440кН∙см
=440кН∙см
2.Определяем требуемый момент сопротивления из формулы (21.10)
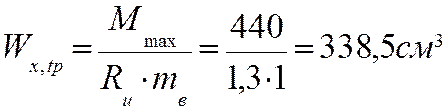
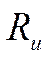 - 13МПа
= 1,3
- 13МПа
= 1,3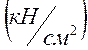 - расчетное сопротивлениеие древесины –
сосна (табл.21.2);
- расчетное сопротивлениеие древесины –
сосна (табл.21.2);
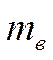 = 1
(табл.20 ) коэффициент, учитывающий температурно – влажностные условия,
отапливаемое помещение А1 (табл. 20.4)
= 1
(табл.20 ) коэффициент, учитывающий температурно – влажностные условия,
отапливаемое помещение А1 (табл. 20.4)
3. Задаемся шириной сечения балки в = 10 см, тогда высота сечения
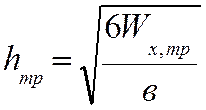 =
=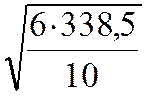 = 14,3см
= 14,3см
принимаем сечение в×h = 10 × 15 см (рис. 20.18)
4. Определяем момент сопротивления
сечения 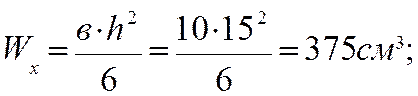
определяем момент инерции сечения 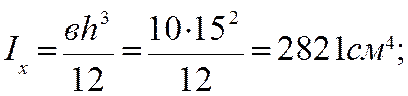
Модуль упругости Е = 100000МПа = 1000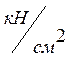 (п.3.6 СНиП II-25-80)
(п.3.6 СНиП II-25-80)
5. Проверяем нормальные напряжения в балке
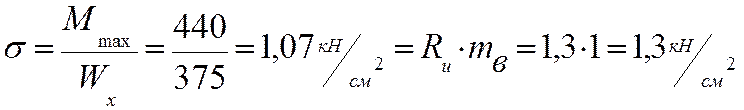 .
.
6. Выполняем проверку прогиба
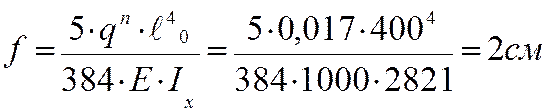
Величина нормативной нагрузки
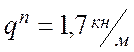 =
=![]()
Пролет балки
![]() = 4м =
400 см;
= 4м =
400 см;
Предельный прогиб (табл.5)
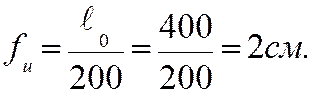
Так как f= ![]() =2см,
=2см,![]() то жесткость балки обеспечена.
то жесткость балки обеспечена.
Вопросы для самопроверки:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.