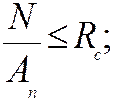Деревянные конструкции. Общие сведения о конструкциях из дерева, страница 7

                                                                                                                (21.3)

б) на устойчивость

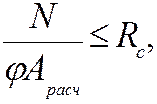                                                                                                          (21.4)

где - расчетное сопротивление древесины сжатию вдоль волокон 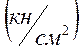 (табл.21.2);

- коэффициент продольного изгиба для древесины определяется по формулам (21.7) или (21.8) в зависимости от гибкости элемента формула (21.5);

Гибкость элементов цельного сечения определяют по формуле

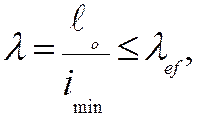                                                                                                    (21.5)

где - расчетная длина элемента (см);

 – минимальный  радиус инерции принимается из  и  (см).

           Расчетную длину элемента   следует определять умножением его длины   на коэффициент

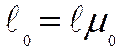                                                                                                             (21.6)

 - коэффициент, принимаемый по п. 4.21 СНиП 2-25-80.

- придельная гибкость сжатого элемента (табл.21.7)

При гибкости элемента

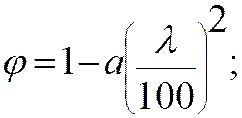                                                                                            (21.7)

 при гибкости элемента

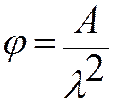           ,                                                                                                  (21.8)

 - площадь нетто поперечного сечения элемента (см);

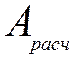- расчетная площадь сечения элемента, принимаемая равной: при отсутствии       ослаблений или ослабляемых в опасных сечениях, не выходящих на кромки (рис.21.4а), если площадь  ослаблений не превышает 25%А, 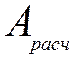 = ,                      где 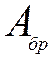- площадь сечения брутто; при ослаблениях не выходящих на кромки, если площадь ослабления превышает 25%A, 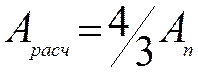; при симметричных ослаблениях, выходящих на кромки (рис. 21.4б), = .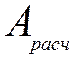

где коэффициент а = 0,8 для древесины и а = 1 для фанеры;

коэффициент А = 3000 для древесины и А = 2500 для фанеры.

          Таблица 21.7

Значение предельных гибкостей (табл.14 СНиП II-25-80)

Наименование элементов конструкций	Предельная гибкость
1.  Сжатые пояса, опорные раскосы и опорные стойки ферм, колоны 2.  Прочие сжатые элементы ферм и других сквозных конструкций 3.  Сжатые элементы связей 4.  Растянутые пояса ферм в вертикальной плоскости 5.  Прочие растянутые элементы ферм и других сквозных конструкций	120 150 200 150 200

Пример 21.1

        Подобрать сечение растянутого стержня из древесины сосна 1-го сорта, в котором действует растягивающее  усилие N=140 кН. Стержень имеет ослабление двумя рядами отверстия диаметром d = 18мм = 1,8 см, выходящих на более широкие стороны стержня (рис. 21.5).

 Решение. Расчетное сопротивление растяжению с учетом коэффициента ослабления  = 0,8, = 8 МПа = 0,8 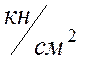 из табл. 21.2.

1. Определяем требуемую площадь сечения с учетом ослабления из формулы (21.9)

                        

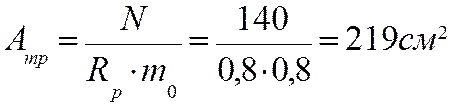
принимаем сечение в×h = 15×17,5 см

Площадь сечения без ослабления.

                        

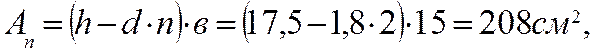
где n =2 отверстия

2. Проверяем напряжение в сечении

                         

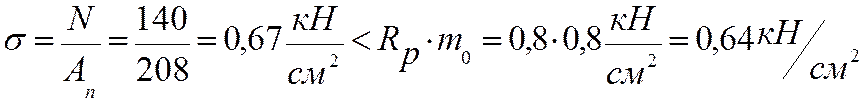
Вывод: прочность стержня, работающего на растяжение обеспечена.

Пример21.2 Проверить сечение центрально сжатого стержня из древесины 2-го сорта, в котором действует сжимающее усилие N = 360 кН. Стержень имеет длину 2м, закреплен с двух сторон шарнирно, ослаблен квадратным отверстием                а×а = 20×20мм (рис. 21.6). Древесина лиственница Сибирская, эксплуатация на открытом воздухе в нормальной зоне.

Решение.

1.  Определяем гибкость стержня в плоскости х-х и у-у.

      Расчетная длина элемента

                 

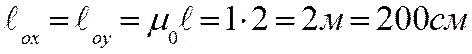
=1 – коэффициент, учитывающий заделку концов стержня, принимается по            (п.4.21). расчетная схема стержня рис. 21.17

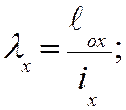
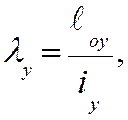         так как сечение квадратное, то радиусы инерции относительно осей х-х и у-у определяем

2. Определяем коэффициент продольного изгиба