Мы используем аппарат с коническими стенками, при этом площадь сечения верхней части сепарационного пространства определяется по соотношению:
|
|
(3.55) |
Площадь сечения грануляционной башни ![]() , что говорит о нереальности уноса частиц
из нее.
, что говорит о нереальности уноса частиц
из нее.
4.3.1.3 Проверка условий псевдосжижения частиц наибольшего диаметра:
а) скорость газа непосредственно у решетки из-за более низкой температуры будет:
|
|
(3.56) |
б) скорость газа в отверстиях газораспределительной решетки:
|
|
(3.57) |
здесь ![]() -
доля живого сечения:
-
доля живого сечения:
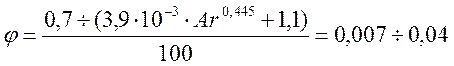 ,
принимаем
,
принимаем ![]() ;
;
в) скорость псевдосжижения частиц максимального диаметра:
|
|
(3.58) |
где ![]() число
псевдосжижения;
число
псевдосжижения;
г) критерий Архимеда:
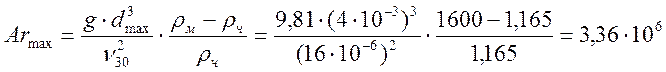
д) критерий Рейнольдса (для момента
начала псевдосжижения ![]() ):
):
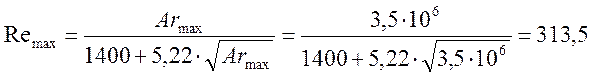
е) скорость газа, необходимая для
сжижения частиц ![]() :
:
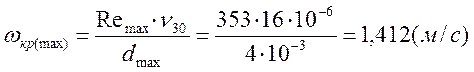
![]()
![]()
19>1,4(м/с), условие выполняется.
3.4.1.4 Выбор шлюзового разгрузителя.
Найдем объемный расход продукта:
|
|
(3.59) |
где ![]() /4, стр. 142/ – насыпная плотность аммиачной селитры.
/4, стр. 142/ – насыпная плотность аммиачной селитры.
По методическим указаниям /14, стр.27/ выбираем разгрузитель ПШ1-450 с характеристиками:
|
Производительность,
|
Объем
ротора, |
Частота вращения ротора, об/мин |
Мощность привода, кВт |
|
5,9-55,8 |
0,05 |
2,1-20 |
2,2 |
3.4.2. Тепловой баланс аппарата.
Аммиачная селитра в зависимости от температуры существует в пяти различных кристаллических модификациях, термодинамически устойчивых при атмосферном давлении. Каждая модификация существует лишь в определенном интервале температур, и переход из одной модификации в другую происходит выделением (поглощением) тепла.
Из /3, стр. 143/ находим теплоты
модификационных превращений: ![]()
![]()
![]() .
.
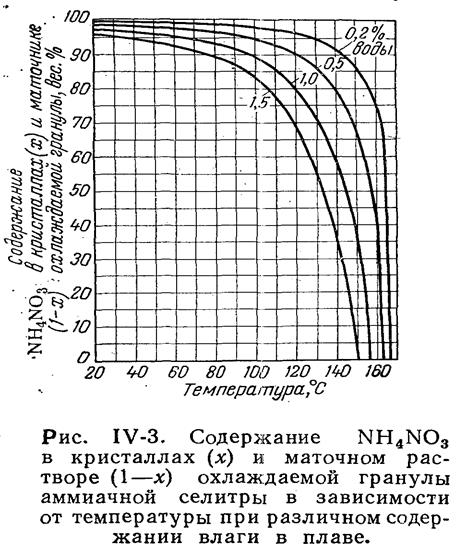
Согласно рис. 4-3, /15, стр. 99/, при охлаждении
капель плава принятой концентрации до ![]() в
условиях протекания процесса до состояния равновесия должно выкристаллизоваться
в
условиях протекания процесса до состояния равновесия должно выкристаллизоваться
![]() вещества. Учитывая отклонение
действительного процесса от реального, принимаем x=0,9
вещества. Учитывая отклонение
действительного процесса от реального, принимаем x=0,9
3.4.2.1 Уравнение баланса для кипящего слоя.
|
|
(3.60) |
где ![]() -
теплоемкость твердой аммиачной селитры.
-
теплоемкость твердой аммиачной селитры.
![]() ,
,
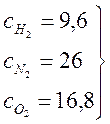
![]() ), /3, таб. 5.1, стр. 249/
), /3, таб. 5.1, стр. 249/
![]()
Переводим из мольной теплоемкости в массовую:
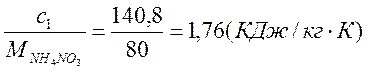 ,
,
![]() /3/
/3/
Рассчитаем количество теплоты, выделившееся в результате охлаждения гранул в кипящем слое:
![]()
3.4.2.2 Уравнение теплового баланса зоны полета.
Теплота, выделившаяся в ходе полета:
|
|
(3.61) |
Количество теплоты, полученное воздухом равно количеству теплоты, отданному селитрой:
![]() .
.
Найдем из последнего уравнения
температуру воздуха на выходе из грануляционной башни, ![]() :
:
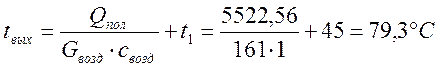
Определим плотность орошения:
|
|
(3.62) |
3.4.2.4 Для определения высоты и времени падения капель:
а) определим количество тепла, отводимого от гранулы в полете:
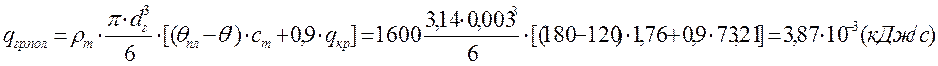
б) найдем критерий Архимеда:
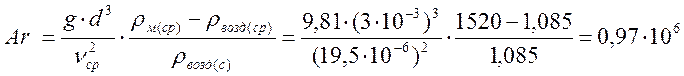 ,
,
где 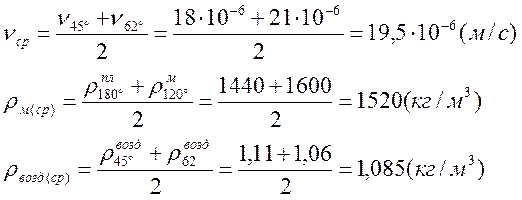 , /3/
, /3/
в) определим Рейнольдс витания:
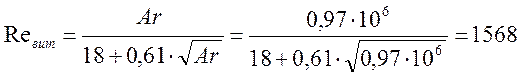 ,
/15, стр51/;
,
/15, стр51/;
г) найдем скорость витания частицы:
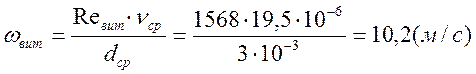 ;
;
д) определим реальные скорость и критерий Рейнольдса частицы с учетом действия потока воздуха:
![]()
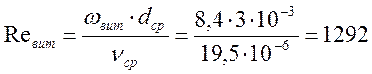
по рис.3-2, /15, стр.108/ найдем критерий
Нуссельта для частицы диаметром ![]() :
:
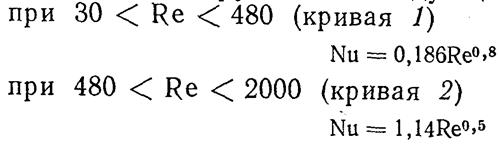
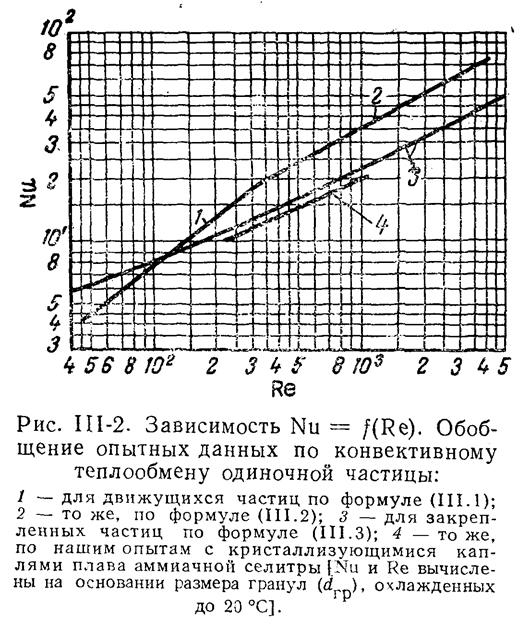
по рисунку определили, что Nu=40;
г) найдем коэффициент теплоотдачи от
гранулы к воздуху, ![]() :
:
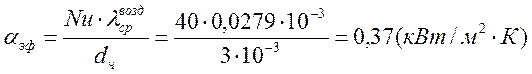 ,
,
где 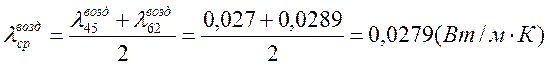 ;
;
д) определим время полета:
|
|
(3.63) |
здесь:
![]() -поверхность
одной гранулы;
-поверхность
одной гранулы;
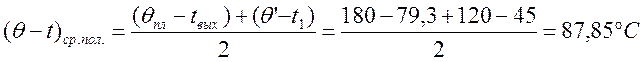 -
средняя разность температур воздуха и гранул в зоне полета (может быть принята
как средняя арифметическая /3, стр. 108/)
-
средняя разность температур воздуха и гранул в зоне полета (может быть принята
как средняя арифметическая /3, стр. 108/)
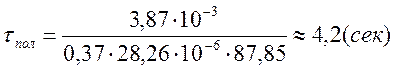
е) определим высоту полета:
![]()
Объединим все данные по тепловому расчету башни в таблицу №3
Таблица теплового баланса
Таблица 3.4.1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.