Распространение радиоволн в тропосфере, страница 8

Функцией автокорреляции R(τ) называют величину, определяемую формулой:

                                        ,                                             (11.33)

где черта означает операцию усреднения во времени.

Из структуры формулы следует, что функция автокорреляции представляет собой среднее по времени значение произведения     функций, разделенных промежутком времени τ. Функция автокорреляции характеризует статистическую связь между значениями случайной величины, разделенными интервалом τ. Если τ®0, то функция автокорреляции стремится к максимальному значению 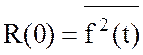. По мере роста τ, R(τ) монотонно уменьшается.

На практике удобнее пользоваться относительным значением функции автокорреляции или коэффициентом автокорреляции, определяемым формулой:

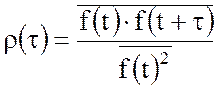
                                          ,                                      (11.34)

который при τ = 0 принимает значение r(0) = 1 и стремится к нулю по мере роста τ.

В реальных условиях уже при конечном значении τ, функции f(t) и   f(t+ τ) можно считать статистически независимыми. В этом и заключается избирательность замираний во времени.

Свойство пространственной избирательности заключается в том, что характер замираний сигнала при одновременном приеме его в пунктах, удаленных на расстояние l, делается все более независимым по мере роста l. Начиная с некоторого  значения разнесения антенн l_кр, замирания делаются практически независимыми. Объясняется это тем, что радиоволны, воздействующие на разнесенные антенны, создаются в несколько различных условиях в пределах общего объема рассеяния.

Обозначим через f₁(t) случайную функцию, характеризующую процесс замираний в месте расположения первой антенны, а f₂(t) – то же, для второй.

Относительной функцией взаимной корреляции (или просто коэффициентом корреляции) называют величину:

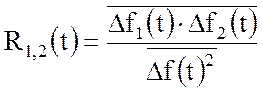                               .                                      (11.35)

При l = 0  R_1,2(0) = 1, а при возрастании l монотонно стремится к нулю.

Экспериментальные данные показывают, что при тропосферном распространении и разнесении антенн на расстояние порядка l =100l коэффициент корреляции весьма мал и замирания сигнала у разнесенных антенн протекают независимым образом.

По тем же причинам при одновременном приеме двух частот, излучаемых одним и тем же передатчиком и отличающихся на величину ∆f, характер замираний, принимаемых на этих частотах сигналов, будет тем более независимым, чем больше расстройка. Экспериментальные данные показывают, что при рабочей частоте f = 2,3 ГГц, при ∆f = 2 МГц коэффициент корреляции составлял R(∆f) = 0,4, а при ∆f = 4 МГц он уменьшается до значения R(∆f) ≈ 0,1. В этом проявляется свойство частотной избирательности замираний.

Свойства пространственной и частотной избирательности замираний широко используются в практике радиосвязи для борьбы с искажениями сигналов, обусловленными замираниями.

Обозначим через S₁ вероятность того, что при приеме на одну антенну сигнал упадет ниже порогового значения Е_мин, при котором еще возможен уверенный прием сигналов. Величина S₁ связана с ранее введенным обозначением Р(Е_мин) соотношением:

.                                  (11.36)

Если, к примеру, S₁ = 10%, то это значит, что сигнал будет уверенно приниматься в течение 90% времени работы линии радиосвязи.

При приеме на две разнесенные антенны вероятность того, что одновременно и на первой и на второй антеннах сигнал окажется ниже порогового значения, можно найти, применяя известную в теории вероятностей теорему о совмещении независимых событий. При этом предполагается, что антенны разнесены друг относительно друга на такие расстояния, при которых замирания протекают независимым образом. Эта теорема гласит, что если S₁, S₂ и т.д. представляют собой вероятности событий, то вероятность одновременного наступления этих событий равна произведению вероятностей этих событий.