Распространение радиоволн в тропосфере, страница 4

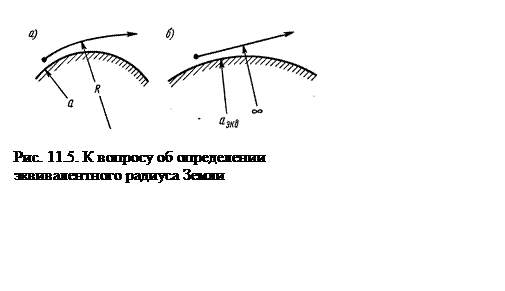
Математически условие эквивалентности имеет вид:

,

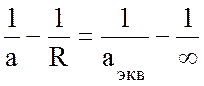где  а – радиус Земли, откуда эквивалентный радиус Земли равен:

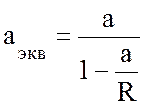                               .                                                  (11.10)

      В случае нормальной рефракции   а_экв = 8500 км.   Для учета рефракции во всех формулах, где фигурирует радиус Земли, нужно подставлять эквивалентное значение. Например, при определении расстояния прямой видимости в формуле (10.12). С учетом рефракции формула  примет вид:

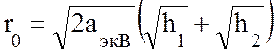.                                              (11.11)

Для случая нормальной рефракции:

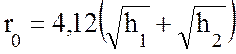                     ,  км,                                        (11.12)

где  h₁ и h₂ – в м.

 

11.4. Дальнее тропосферное распространение

Исследуется явление тропосферного рассеяния. Рассмотрены вопросы использования этого явления для дальней радиосвязи на УКВ.

 

Микроструктура тропосферы. Исследования тропосферы с помощью метеорологических зондов показали, что изменение индекса преломления с высоты не может быть описано монотонно-гладкой кривой.

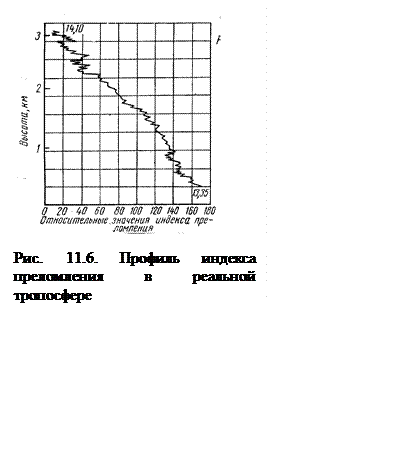 На рис. 11.6. показан образец записи высотного профиля индекса прелом-ления, на котором видны беспо-рядочные мелкие выбросы. Причиной этому является наличие в тропосфере мелких локальных неоднородностей, порождаемых вихреобразным движени-ем воздушных масс.  При достижении скорости движения, превышающей некоторое критическое значение,  упо-рядоченное движение воздушной массы нарушается, принимая вращающийся (вихреобразный) характер. Из теории газов известно, что большие вихри спу-стя некоторое время после зарождения неизбежно распадаются на более мелкие, пока в самых малых вихрях  кинетическая энергия вращения не превратится за счет преодоления сил вязкости в тепло.  Следствием этого процесса в локальной области тропосферы происходит изменение температуры и давления газа, а, значит, и коэффициента преломления. Таким образом, локальная область приобретает характер неоднородности. Распространяя рассуждения на всю массу тропосферы, можно заключить, что тропосфера в целом представляет собой совокупность огромного числа мелких неоднородностей.

      Время существования неоднородностей исчисляется временем от долей секунды до десятков секунд. В локальной области тропосферы в результате непрерывного движения одна неоднородность замещается другой с иным коэффициентом преломления. Поэтому в этой области коэффициент преломления испытывает быстрые хаотические изменения (флуктуации). Тогда размер неоднородности оценивается статистической связью между флуктуациями диэлектрической проницаемости (коэффициента преломления) в двух точках, удаленных на расстоянии  r.    Как известно из курса теории вероятностей, статическая связь двух случайных процессов описывается функцией корреляции:

                                         ,

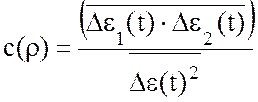где  ∆ε₁(t) и ∆ε₂(t) – флуктуации диэлектрической проницаемости относительно некоторого среднего значения.

Здесь черта означает усреднение по времени. Средним размером неоднородности называют величину:

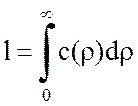, м.                                                     (11.13)

По своему физическому смыслу величина  l в первом приближении определяет радиус сферы, на которую распространяется сильно выраженная статистическая связь. Если рассматриваемые точки находятся на очень небольшом расстоянии     друг   от  друга, то флуктуации в них  протекают синхронно и  с(r) ® 1. В этом случае можно говорить, что обе эти точки находятся в пределах одной неоднородности. В противном случае процессы в этих точках протекают независимым образом и с (r) ® 0. Это означает, что точки принадлежат разным неоднородностям.