Распространение радиоволн в тропосфере, страница 2

     Для удобства использования в вычислительных операциях и измерениях вместо коэффициента преломления вводят величину, называемую индексом преломления, который показывает, на сколько миллионных долей коэффициент преломления отличается от единицы:

N = (n - 1) 10⁶.                                     (11.1)

Из курса молекулярной физики известно, что индекс преломления можно выразить через основные параметры газа как:

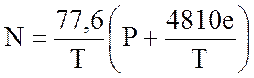                     .                                   (11.2)

Эта формула справедлива для длин волн более 0,1 мм. На более коротких волнах, тем более в оптическом диапазоне, молекулы воды обладают столь высокими инерционными свойствами, что перестают влиять на оптические свойства тропосферы. Поэтому на этих частотах формула для N принимает вид:

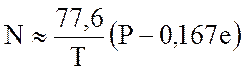                               .                                    (11.3)

         Свойства тропосферы подчиняются аддитивному закону, т.е.  результирующий коэффициент преломления определяется как сумма коэффициентов преломления отдельных парциальных составляющих смеси. Так как удельный вес паров воды (влажность) убывает с высотой, то и  результирующий коэффициент преломления также убывает.

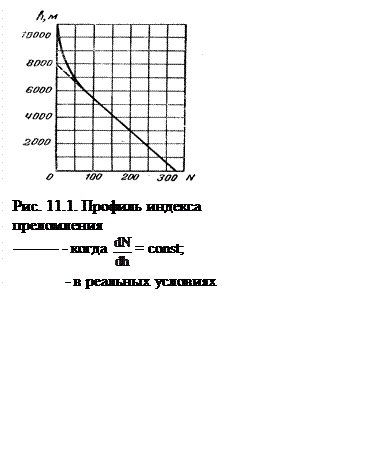У нормальной тропосферы градиент индекса преломления постоянен по всей ее толще, а величина самого индекса у поверхности Земли равна примерно 300. При этих условиях вертикальный профиль индекса преломления имеет вид, показанный на рис. 11.1.

При условии постоянства градиента индекса преломления на высоте 8 км индекс преломления должен был бы превратиться в нуль (пунктирная линия). В действительности, начиная с высоты 7 км, скорость убывания индекса уменьшается, и на профиле появляется криволинейный участок.

В реальных условиях форма вертикального профиля индекса преломления отличается от идеализированной, так как тропосфера постоянно находится под воздействием метеорологических условий. В ряде случаев на профиле могут появиться участки с положительным градиентом.

Таким образом, тропосфера, в общем, является неоднородной средой, у которой коэффициент преломления изменяется с высотой.

 

11.3.  Тропосферная рефракция радиоволн

Обсуждаются вопросы распространения радиоволн в неоднородной тропосфере.

 

Вследствие непостоянства коэффициента преломления по высоте, радиоволны, распространяющиеся в тропосфере, в соответствии с законами оптики испытывают плавное искривление траекторий. Это  явление называется тропосферной рефракцией. Определим условия, влияющие на степень кривизны лучей. Представим толщу тропосферы, состоящей из воображаемых очень тонких плоских слоев с постоянным коэффициентом преломления   n_i, которые удалены друг от друга на очень малое расстояние  dh. В этом случае волны будут испытывать ряд последовательных преломлений на границах между слоями. Угол преломления можно определить из закона Снеллиуса:

n₁ sinj₁ = n₂ sinj₂ = n₃ sinj₃ = . . . n_n sinj_n.                   (11.4)

       Траектория волны в этом случае будет представлять собой ломаную линию. Если устремить число слоев к бесконечности, а расстояние между ними к нулю, то траектория волны станет гладкой кривой, что имеет место в реальных условиях (рис. 11.2.).

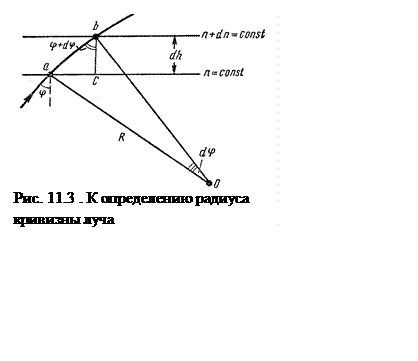         Определим радиус кривизны луча. Для  простоты представим, что траектория волны является частью окружности с радиусом  R. Из всей толщи тропосферы выделим два очень тонких воображаемых слоя с постоянными коэффициентами пре-ломления  n  и  n + dn, отстоящих друг от друга на очень малом рас-стоянии  dh (рис. 11.3.). По опре-делению дуга  аb= R sin dj » R dj. Из-за бесконечно малых размеров дуга аb может быть заменена прямой, а  треугольник  аbс можно считать прямоугольным. Из  треугольника аbс: 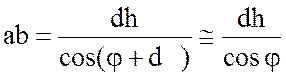 , откуда:

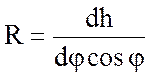          .                        (11.5)