Распространение радиоволн в тропосфере, страница 6

      При достаточно малом объеме рассеяния, что реально часто имеет место, формула для множителя F принимает окончательный вид:

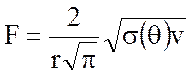                                           .                                              (11.23)

      Из формулы (11.20) видно, что для расчета мощности на входе приемника, создаваемой приходящей волной из объема рассеяния, необходимо знать величину объема рассеяния и эффективную удельную площадь единицы объема рассеяния. На УКВ ширина главного лепестка диаграммы направленности антенны относительно мала. Поэтому объем рассеяния может быть с достаточно высокой точностью определен как фигура, образованная пересечением пространственных диаграмм направленности передающей и приемной антенн. Объем рассеяния как часть мелко неоднородной тропосферы описывается статистическими понятиями. Поэтому для определения  s (q) необходимо знание корреляционной функции  с(r). В литературе имеются различные аппроксимации этой функции известными статистическими законами. Имеются также сведения об экспериментальном определении этой величины.

 

11.5 . Замирания сигналов при тропосферном распространении

 Рассмотрены проблемы, связанные с замираниями радиосигналов на линиях тропосферной связи.

 

Как было показано выше, структура поля в пункте приема имеет интерференционный характер. В результате этого отноше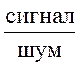ние  на входе приемника также подвержено замираниям, что уменьшает помехозащищенность  радиолинии. Нарушения в работе радиолинии возникают тогда, когда отношение 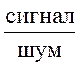 становится ниже некоторого минимального уровня. В конечном счете это отношение является критерием помехозащищенности радиолинии от воздействия помех.

Количественно замирания оцениваются рядом показателей. Это медианный уровень, глубина замираний, частота замираний и средний период замираний. Все эти величины имеют вероятностно-статистический характер. Медианным уровнем сигнала называется уровень, превышаемый в течении 50% времени наблюдения. Поэтому эта величина также называется средним по времени (рис. 11.8.).

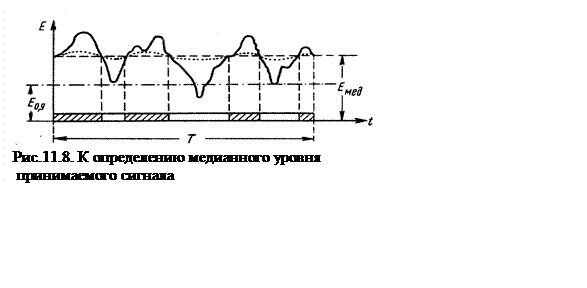 Глубину замираний можно определить весьма условно, учитывая хаотический характер замираний. Нельзя глубину замираний оценивать отношением максимального уровня к минимальному за время Т, так как отдельные пики могут достичь весьма больших значений с весьма малой вероятностью. С другой стороны, глубокие замирания маскируются шумами. Поэтому под глубиной замираний принято считать разность уровней с вероятностью 0,1  и 0,9  , выраженную в дБ. Формально это выражается как:

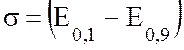                                         ,  дБ.                                        (11.24)

      Частота замираний определяется по числу пересечений медианного уровня. Например, если за время Т число перечислений медианного уровня составляет 10, то частота замираний f_срравна 5 периодов за время Т или   Гц. Средний период:

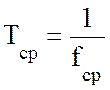                                         .                                                           (11.25)

Наиболее полную характеристику замираний дает функция распределения уровней сигнала. Образец функции приведен на рис. 3.9.

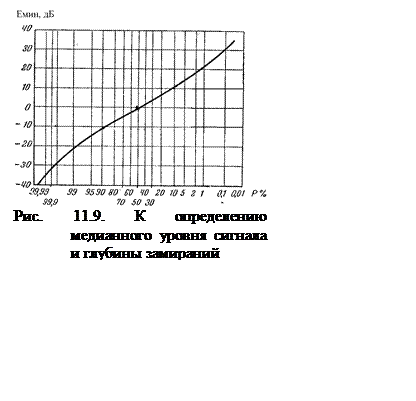Здесь на оси абсцисс отложено время, в течение которого превы-шается уровень, отложенный на оси ординат. Время берется в процентах по отношению к времени наблюдения, а уровни сигнала на оси ординат отло-жены в децибелах по отношению к медианному уровню. Воспользовав-шись графиком рис. 11.9., можно опре-делить медианный уровень сигнала, а также глубину замираний.

           Многолетние наблюдения за флуктуациями сигнала на тропосфер-ных радиолиниях показали, что замирания сигнала имеют сложный характер. Это проявляется в том, что на относительно медленные изменения уровня сигнала, средний период которых составляет десятки секунд накладываются быстрые колебания со средним периодом от нескольких секунд до долей секунды. Многочисленные измерения показали, что медленные замирания подчиняются чаще всего логарифмически нормальному закону, а быстрые – закону Релея.