Распространение радиоволн в тропосфере, страница 7

В случае нормального закона плотность распределения случайной величины определяется из формулы:

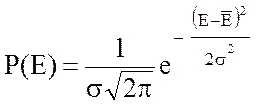          ,  ,                                         (11.26)

где Е – мгновенное значение случайной величины напряженности поля радиоволны, Ē – математическое ожидание, σ – стандартное отклонение, σ² – дисперсия.

Напомним, что математическим ожиданием случайной величины называется ее среднее значение, определяемое из формулы:

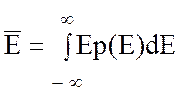                     ,                                   (11.27)

где  р (Е) – плотность вероятности величины Е.

          Стандартным отклонением называется такое отклонение от медианного , вероятность которого составляет 16% и 84%.

В случае логарифмически нормального закона плотность распределения случайной величины определяется из формулы:

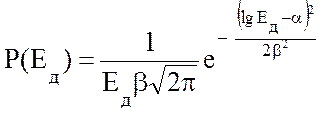                ,,                   (11.28)

где    Здесь случайной величиной является действующее значение напряженности поля радиоволны.

Для быстрых замираний чаще всего справедлив закон Релея, где плотность распределения действующего значения напряженности поля определяется из формулы:

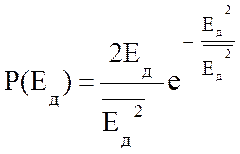          ,      .                                         (11.29)

На радиолиниях, работающих в условиях замираний и радиопомех, существуют нормы на время надежной (без нарушений) работы. Так, на линиях коротковолновой магистральной радиосвязи время исправной работы при круглосуточной работе радиолинии составляет 90% при условии, что вероятность ошибок не превышает 10^-3. Если время исправной работы радиолинии известно, то соответствующее ему значение уровня полезного сигнала можно определить, воспользовавшись функцией распределения уровней сигнала. Для этого формулы (11.26) и (11.29) нужно представить в интегральной форме.

Интегральная форма нормального закона имеет вид:

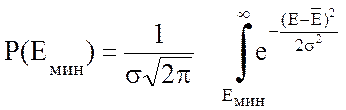.                      (11.30)

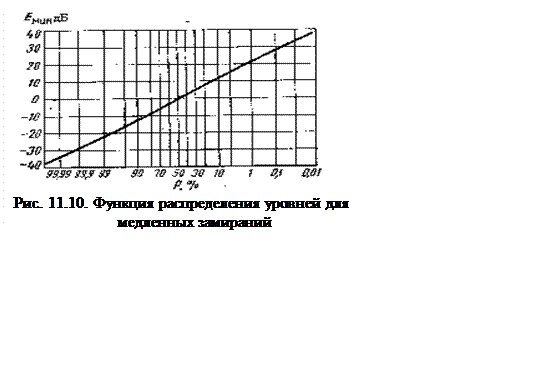
График функции приведен на рис. 11.10.

Закон Релея в интегральной форме выражается формулой

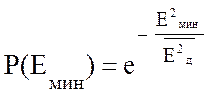                              .                                                     (11.31)

В качестве примера определим пороговое значение уровня сигнала в условиях быстрых замираний, если время исправной работы радиолинии составляет 90%. Для этого обратимся к рис.11.11., на котором изображена функция распределения уровней для быстрых (релеевских) замираний. Как видно из рис.11.11., пороговый уровень должен составлять +8 дБ по отношению к медианному уровню, т.е. превышать медианный уровень в 2,5 раза.

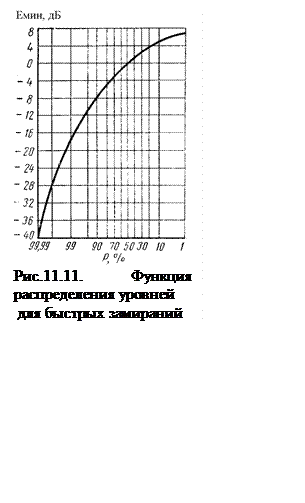Закон Релея в чистом виде реализуется далеко не во всех случаях. В тех случаях, когда поле в пункте приема представляет собой результат интерференции колебаний с посто-янной амплитудой и фазой и множества коле-баний с произвольными амплитудами и случай-ными фазами, выполняется так называемый обобщенный закон Релея или закон Райса. При-равняв амплитуду постоянной составляющей к единице и обозначив отношение квадрата действующего значения суммы “рассеянных” составляющих к действующему значению пос-тоянной составляющей через k², функцию распределения для закона Райса можно представить в виде:

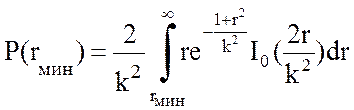,                    (11.32)

где  r – относительное значение амплитуды результирующего поля, а I₀(x) –функция Бесселя первого рода нулевого порядка.

Действие того или иного аналитического закона распределения можно установить только на основании экспериментальных данных. Часто для определения требуемой мощности передатчика для выполнения нормы на время исправной работы радиолинии используют функцию распределения, полученную на данной радиолинии экспериментально.

Избирательный  характер замираний. Все виды замираний, независимо от диапазона волн и способа распространения, обладают свойствами временнóй, пространственной и частотной избирательности.

Под избирательностью замираний во времени понимают следующее. Допустим, что зависимость подверженного замираниям поля от времени выражается случайной функцией f(t). Пусть f(t+τ) выражает ту же зависимость, в которой начало отсчета сдвинуто на промежуток времени τ.