Распространение радиоволн в тропосфере, страница 3

            Произведение dj cosj   найдем из закона Снеллиуса для точек а и b траектории волны:

n sinj = (n + dn) sin (j + dj ).

Раскроем скобки:

n sinj =n sinj cosdj + n cosj  sindj  +  dn sinj  cosdj  + dn cosj  sindj .

Из-за малости угла dj имеем: sin dj » dj ,  cos dj » 1 и dn ∙ dj » 0  как бесконечно малая второго порядка. В итоге 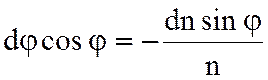  ,  и

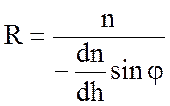.                                               (11.6)

       С учетом того, что угол j в реальных условиях достаточно близок к 90⁰, а величина n близка к единице, окончательное выражение для радиуса кривизны луча будет иметь вид:

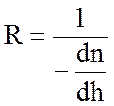                                                            .                                                           (11.7)

        На основании формулы (11.7) можно сделать вывод, что кривизна луча определяется только градиентом коэффициента преломления и не зависит от абсолютных величин р, Т, е. При переходе от  n  к  N формула  (11.7) принимает вид:

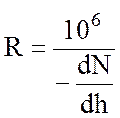.                                           (11.8)

       В реальных условиях величина  постоянно испытывает хаотические изменения, что связано с изменениями температуры, давления и влажности воздуха. Поэтому кривизна траектории также подвергается непрерывным изменениям, причем на разных высотах по-разному. В результате этого траектории могут принимать весьма разнообразную форму. При определенных условиях траектория может принять отрицательную кривизну. Это означает, что волна удаляется от Земли. Это явление назвали отрицательной рефракцией. При распространении прямых волн (УКВ) над сферической Землей положительная рефракция способствует увеличению напряженности поля в точке приема, а отрицательная - уменьшению. В случае положительной рефракции градиент коэффициента преломления имеет отрицательный знак, а в случае отрицательной рефракции - положительный.

       По степени кривизны луча при положительной рефракции различают несколько видов рефракции:

      1. Слабая     < - 4,3×10 ^–2,    

      2. Нормальная   = - 4,3×10 ^–2,                                                       (11.9)

      3. Критическая   = - 0,157,    

      4. Сверхрефракция   > 0,157,     .

Траектории лучей при различных видах рефракции изображены на рис11.4.

       В условиях сверхрефракции луч испытывает полное внутреннее отражение на той высоте, где градиент индекса преломления становится больше, чем  - 0,157 .  Могут иметь место условия, когда луч испытывает ряд последовательных отражений от тропосферы и Земли, в результате чего возможна радиосвязь на расстояниях, значительно превышающих расстояние прямой видимости. Как говорят, возникает тропосферный волновод. Этим объясняется дальнее распространение на УКВ и явление миража в оптическом диапазоне (рис.11.4.). Сверхрефракция возникает в основном в результате необычно резкого перепада влажности воздуха, что чаще всего имеет место в прибрежных районах и пустынях. Отождествление сверхрефракции с волноводом имеет место не только образный смысл, но и достаточно строгую основу. Дело в том, что тропосферный волновод имеет критическую частоту точно так же, как и металлический. Из опыта известно, что сверхрефракция возникает на волнах, длина которых не превышает 2 м, т. е. в диапазоне УКВ.

        Учитывая хаотический характер изменения кривизны луча, в практических расчетах используют значение градиента индекса преломления для нормальной тропосферы:

                                                   ,  .

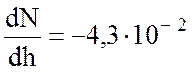Радиус кривизны луча в этом случае будет равен 25 тысяч километров (формула 11.8.).

      Для учета рефракции при расчете напряженности поля в точке приема, при определении расстояния прямой видимости и т. д.  вводят понятие эквивалентного радиуса Земли. Идея заключается в том, чтобы свести задачу о распространении волны над сферической поверхностью Земли в условиях рефракции  к задаче о прямолинейном распространении волны над сферической поверхностью Земли с эквивалентным радиусом. Условием эквивалентности обеих задач является постоянство относительной кривизны луча. Смысл метода иллюстрирован рисунком 11.5.