Дифференциальные уравнения. Общие понятия

Дифференциальные уравнения. Общие понятия.

Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные, наибольший порядок которых равен n, называется обыкновенным или просто дифференциальным уравнением порядка n.

                             

          Везде в уравнении неизвестные функции по производной зависят от единственной переменной x. Не давая определение другому виду дифференциальных уравнений – уравнениям в частных производных, укажем, что в этом случае неизвестная функция зависит от нескольких переменных . Ниже рассматривается только об  обыкновенные или просто дифференциальные уравнения.

 Функция  называется решением дифференциального уравнения , если при подстановке этой функции в уравнение последнее превращается в равенство.

          Рассмотрим уравнение первого порядка:

И предположим , что оно решено относительно производных. Тогда имеем

                        или

Уравнение - уравнение для первообразной. Его решение, как известно можно записать в виде:

                        или   ,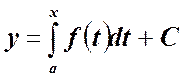

где [a, b]- интервал на котором задано уравнение и первообразная. Таким образом, решение уравнения  можно назвать множество первообразных или общим решением (частным решением будет одна первообразная, подученная при фиксированном С). Кроме того, что общее решение можно называть общим интегралом. С геометрической точки зрения общее решение- совокупность интегральных кривых. И, наконец, рассмотрим геометрический смысл дифференциального уравнения первого порядка .

    Как уже было отмечено, общее решение  - множество интегральных кривых на плоскости  x, y, а  - производная или геометрически касательная в точке . Эти касательные образуют поле направлений.

          Аналогичным образом строится общее решение уравнения второго порядка.

Пусть . Полагая , имеем

          Уравнение для первообразной :

Даже           - также уравнение первообразной  и ее решение – общее решение уравнения второго порядка:

                             

1.  Задача Коши для уравнений 1 и 2 порядка.

Дифференциальное уравнение  имеем единственное решение, соответствующее данному начальному условию., если - непрерывная функция, имеющая частную производную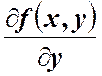      

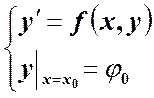
Для дифференциального уравнения второго порядка  также имеют место те же условия дифференцируемости  по y и , при которых решение, удовлетворяющее паре начальных условий,    

                                                                               

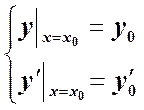
, имеет единственное решение             

                                                          

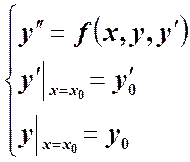
2.  Дифференциальное уравнение 1 порядка с разделяющими переменными.

Уравнение вида  называется уравнением с  разделяющими переменными.

 Разделяем левую и правую части уравнения N(y)P(x):

    

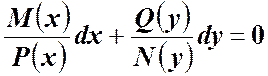
и получим уравнение с  разделяющими переменными, не отличающееся от уравнения для первообразной:

                         .

Поэтому при равенстве дифференциалов имеем равенство первообразных.

               И в этом и в другом случаях общий интеграл или общее решение имеет вид:

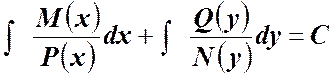
3. Однородные уравнения.

 Функция  называется однородной функцией n-ого порядка, если выполняется равенство

Уравнение вида   называется однородным, есл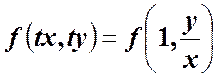и

  и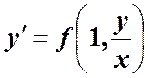

Данное уравнение сводится к уравнению с разделяющимися переменными

заменой функции y=x u, где u(x)- новая неизвестная функция и . Подставив выражения для y и для в однородные уравнения получим .

Тогда 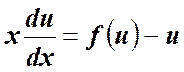   -  искомые уравнения с разделяющимися переменными.

4.  Линейные уравнения.

 Линейным уравнением 1 порядка называется уравнения вида:

                    ,

где 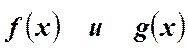- известные функции.

Иначе это уравнение называют линейным неоднородным уравнением с правой частью. Уравнение  называют линейным однородным уравнением(без правой части).

  Его общее решение имеет вид 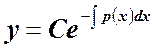. Для нахождения общего решения уравнения с правой частью  применим прием, который называется методом вариаций произвольной постоянной. Он состоит в следующем: решение  уравнения будем искать в виде :

                                         =

и, получив это решение, свяжем его с решением однородного уравнения и получим общее решение линейного уравнения с правой частью. Подставив его в это уравнение, убедимся, что оно является искомым. Итак,

=

Так как - решение, то оно удовлетворяет уравнению с правой частью.

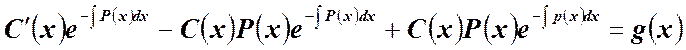
и

.

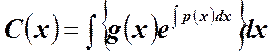 Тогда общее решение имеет вид

                              .

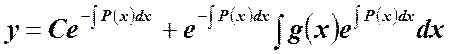 Убедимся в том, что это решение имеет место:

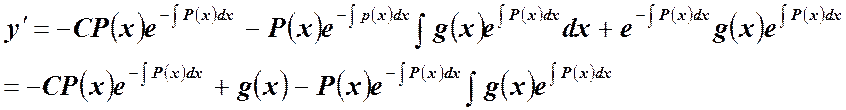
 Подставив общее решение и его производные в уравнение , получим

 - искомое равенство.

5. Частные случаи уравнений второго порядка.

а) - в уравнении отсутствует неизвестная функция и ее первая производная. Если это уравнение разрешено относительно  , то имеем:

 , где - известная функция.

Пусть , тогда  и вместо уравнения  второго порядка

 Имеем

  - уравнение для первообразной .

 Его общее решение:

          ,

так как , то получаем еще одно уравнение для первообразной y

                                        ,

                    ,

которое и является общим решение.

б) - уравнение не содержит неизвестной функции.

Введем  и  в начальное уравнение и получим

                   

уравнение 1 порядка относительно неизвестной функции . Решив это уравнение:

                    ,

заменим в нем :