Дифференциальные уравнения. Общие понятия, страница 3

6. Явный вид определителя Вронского.

 Определитель Вронского  на некотором множестве          имеет вид: =

=, где  и - линейно независимые частные решения уравнения

 ,

то есть:

          ;  

Умножив первое уравнение на , второе на  и вычитая из первого уравнения второе уравнение, получим:

         

или

                 ,

            ,                   =       ,

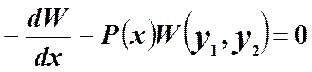
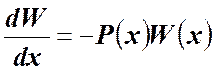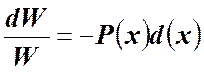что и требовалось доказать.

7. Нахождение общего решения уравнения второго порядка при одном известном решении.

  Пусть y- любое решение уравнения ,

Отличное от известного . Тогда общее решение  имеет вид:

                             

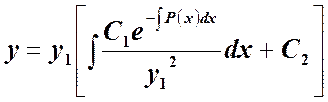
Так как ==, то, разделив это равенство на ,  получим:

                      

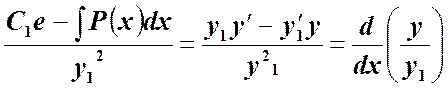
Уравнение с разделяющимися переменными, общее решение интеграл которого:

                             

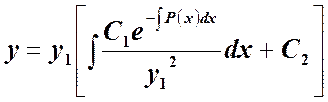
является общим (решением) потому, что  и - линейно независимы и содержат две произвольные постоянные.

8. Неоднородные (с правой частью) линейные уравнения второго порядка.

Теорема об общем решении.

Если известно какое-то частное решение неоднородного уравнения, то его общее решение равно сумме этого решения и общего решения однородного уравнения.

 Итак,  известно - частное решение неоднородного уравнения

                    и

                              - общее решение однородного уравнения

                             

Тогда, требуется доказать, что

                              -

общее решение неоднородного уравнения, то есть, что при надлежащем выборе значения постоянных  получится решение , удовлетворяющее двум начальным условиям задачи Коши (в любой точке ).

 Пусть ,           ,     ,     ;

,           ,      ,     -

известные постоянные. Тогда для начальных условий получим

;         

Эта система уравнений имеет единственное решение, так как ее определитель- определитель Вронского отличен от нуля для фундаментальной системы функции  и .

          Таким образом, постоянные  в любой точке  принимают определенное значение и решение действительно является общим.

          9. Метод вариации постоянных – метод нахождения частного решения неоднородного уравнения может быть найдено методом вариации постоянных.

          В уравнении  известно общее решение неоднородного уравнения . Требуется доказать , что частные решение неоднородного уравнения имеет вид

,

где - известные функции.

    Обозначим  частное решение.

Это решение зависит от двух неизвестных функций , и, следовательно, для их определения требуется два уравнения. Одно из них- исходное уравнение, потому при подстановке решения оно удовлетворяет и второе уравнение задано произвольно.

  Для получения второго уравнения найдем:

                              +

 и покажем что - второе частное решение. При этом

,     

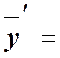
           и

                   

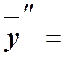
подставим в первое уравнение:

+

 

Первые два слагаемых равны нулю, так как  и - решения однородного уравнения и остается уравнение (первое):

 

и уравнение

,

полученное ранее , из которых определяют производные .

                     ,    

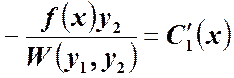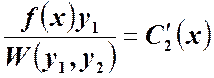
и  искомые    равны

                    ;         

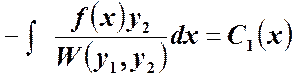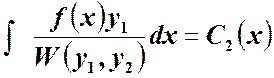
Здесь определитель Вронского - .

Окончательно имеем частные решения

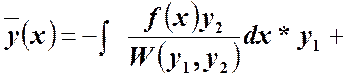
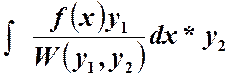
10. Линейные однородные уравнения второго порядка с постоянными коэффициентами. Метод характеристического уравнения.

Таким уравнением является

                              ,

где p и  g- действительные числа.

Общее решение этого уравнения  будем искать следующим образом. Пусть  при фиксированном - одно из частных решений данного уравнения. Тогда при подстановке решения в уравнения имеем