Дифференциальные уравнения. Общие понятия, страница 4

                                       

                                 или

                                       

Последнее уравнение называется характеристическим. Его дискриминант  позволяет рассмотреть три случая. Первый -, тогда  и -  действительные числа и мы имеем два линейно независимых решения ,  и общее решение равно:

                                        

          Второй случай- , т.е.  или 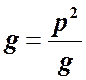 и характеристическое уравнение

                                        

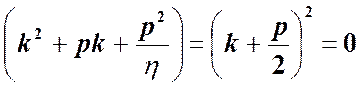
имеет один корень 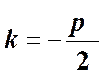  и одно частное решение 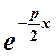. Второе частное решение -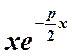. Подставляя последнее в исходное уравнение, получим:

                    =

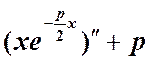
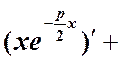
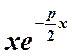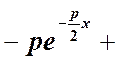
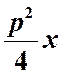
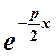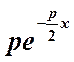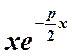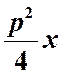
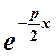+-+=0

В результате получим общее решение

                             

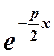
И, наконец, рассмотрим . При этом характеристическое уравнение имеет вид:

                              ,

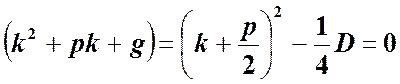                    или

                              ,

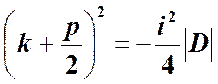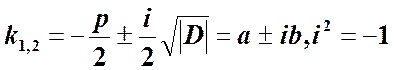
Получаем два линейно независимых частных решения

                             

Тогда общее решение имеет вид

                             

          11. Неоднородные линейные уравнения с постоянными коэффициентами и правой специальной частью.

                                       

    или   ,

                                      ,

где - многочлен n-ой степени.

А.   Рассмотрим уравнение

                             

и его частное решение , где - многочлен той степени, что и . Подставляем частное решение в уравнение

                 

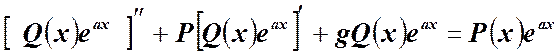
          или             

Приводя подобные слагаемые получим :

                    

Отметим, что - многочлен меньшей степени, чем  и поэтому последнее равенство возможно только в том случае, если , то есть при a, не являющимся корнем характеристического уравнения.

          Рассмотрим три случая:

а) Число a не совпадает с корнями характеристического уравнения. Поэтому из всех значений а рассмотрим лишь те значения, когда  и

В этом случае частное решение:

                 , где =,

а коэффициенты , i=0,1,2,…n находятся из уравнения.

б) Число a совпадает с одним из  корней характеристического уравнения, то есть .

В этом случае:     не является решением:

Как уже показано выше,

                

                               ,

так как многочлен слева не равен многочлену справа( степень многочлена слева на единицу меньше, чем многочлена справа).

          В этом случае частное решение:

                                        .

Подставляем  в исходное уравнение, найдем методом неопределенных коэффициентов числа  для многочлена .

в) В случае, число a  совпадает с обоими корнями характеристического уравнения(когда эти корни одинаковы), частное решение равно:

                                        .

В. Рассмотрим уравнение

                                         .

Если корни характеристического уравнения действительные, то частое решение

                             

Если корни характеристического уравнения действительные, то частное решение

                              ,

где и - многочлены одной степени с . В противном случае, когда корни характеристического уравнения- комплексные числа

                                        ,

не совпадающие с числом , частное решение имеет вид

                             

И, наконец, если комплексное число , заданное правой частью дифференциального уравнения совпадает с одним из корней характеристического уравнения  , то частное решение имеет вид

                              ,

где и - многочлены той же  степени, что и  , коэффициенты которых не известны.