Строительство и архитектура \ Проектирование и эксплуатация нефтехранилищ и автозаправочных станций

Проблемы эффективности производства на северных нефтегазодобывающих предприятиях (доклады и сообщения). Том 2, страница 28

60


ГАЗ

р

С

Н,

-

Тс

\

^         \

Жидкость      "~ _2

--

Rk

Схема притока газа к скважине при наличии подошвенной воды

1.  Давление в газовой части пласта осреднено по вертикали.

2.  Для течения жидкости действительны все допущения без­
напорного движения в гидравлическом приближении.

При таких допущениях установившийся приток газа к скважине при наличии подошвенной воды, соответствующей рисунку, опи­сывается следующей системой уравнений:


S(H-xJ2

«.Cr

dt "

dt~    r Обозначения:


(1)



QLr


(2)


где г - полярная координата;

рат - плотность газа в стандартных условиях;

61


Qr- объемный дебит газа в стандартных условиях;

ц г - вязкость газа;

к - проницаемость пласта;

Рат - стандартное давление; /3 - коэффициент извилистости; уж - плотность жидкости;

£ = ужкк/рк«;1                - малый параметр.

Остальные обозначения понятны из рисунка. Предполагается также, что течение газа следует двучленному закону фильтрации, а газ считается идеальным.

Кроме того, на границах рассматриваемой области должны выполняться следующие условия:

(3)

Условие (3) необходимо для определения констант интегри­рования и дебитов газа и жидкости (в данном случае дебит жидкости равен нулю).

Система (1) - сингулярно возмущенная [3,4]; решение ее отличается от решения вырожденной системы (т.е. при е = 0) наличием т.н. пограничных функций, значительных вблизи границы рассмат­риваемой области и быстро затухающих по направлению внутренней нормали к границе. Отметим также, что величина у погранфункции нулевого порядка всегда равна нулю.

В случае системы (1) легко заметить, что сумма обоих уравнений интегрируется; с учетом третьего и четвертого условий (3) можно записать:

или

Подставляя (5) в первое уравнение системы (1), получим:

62


 (6)

Уравнение (6) - стандартное [5 ], и для его решения естественно было бы применить метод усреднения, однако в данном конкретном случае уже при решении уравнения сравнения первого приближения искомая функция должна находиться из трансцендентного уравнения. Поэтому для решения уравнения (6) применим метод пограничных функций [3,4].Полученное этим методом решение будет иметь сле­дующий вид:

 (8?

д..  МгРатУжГ|+ Но-Ки \^?с                                       (9)

м ^ D     ч

Б

—      r   aT g*

(10)

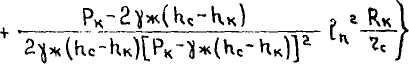
Как видно из (9) и (10), коэффициенты фильтрационных сопротивлений А и В при исследовании на стационарных режимах меняются от режима к режиму, так как в них входит величина he - высота столба жидкости на стенке скважины. Вообще говоря, время образования стационарного конуса жидкости может быть очень большим - во много раз превышающим время исследования скважины. Если предположить, что во время исследования А и В меняются незначительно, то переписав (8) в виде можно обрабатывать результаты исследований в координатах Рс(Рк - Рс) /Qr - Qr.KaK известно, стандартная обработка результатов исследования проводится по зависимости [1 ]:

В качестве критерия успешности обработки можно взять ко­эффициент парной корреляции R.

63


В таблице приведены значения коэффициента парной кор­реляции, полученные при обработке результатов исследований по зависимостям (11) и (12) для некоторых скважин Южно-Соленинского месторождения ГП Норильскгазпром.

Результаты исследований

Номер скважины, год исследования

Коэффициент корреляции R при обработке

по стандартной зави­симости (12)

по зависимости (И)

102 (1987) 102 (1989) 104 (1985) 104 (1990) 105 107 (1983) 109

-0,45 -0,87 -0,8 0,2 0,37 -0,14 -0,59

0,95 0,95 0,98 0,85 0,92 0,92 0,94
Скачать файл