Синтез корректирующих цепей линейных САУ. Часть IV: Методические указания к выполнению курсовой работы по курсу «Теория автоматического управления», страница 3

 

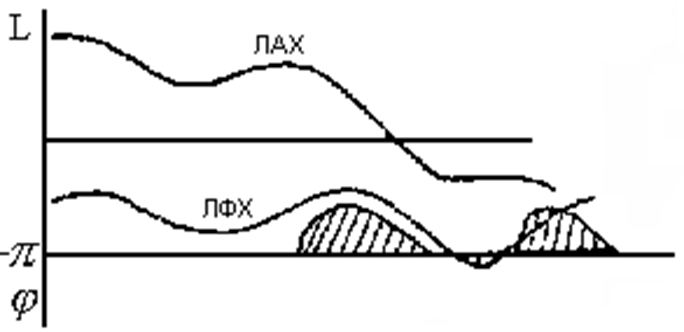
Рис. 5. Запретные области для ЛФХ.

По -кривым можно определить и запретную область для ЛАХ по имеющейся ЛФХ и заданному М. Для этого определяются значения модуля ЛАХ для каждого значения:

.

Синтез последовательных корректирующих

 устройcтв по JIAX.

Если корректирующее устройство включено в главный контур системы последовательно с остальными звеньями, то корректирующее устройство называют последовательным.

Структурная схема скорректированной системы изображена на рис. 6.

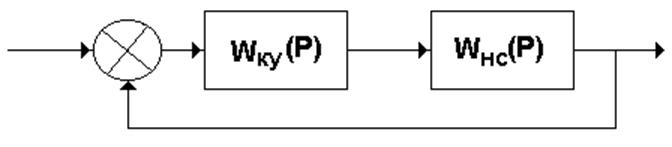
Рис. 6. Структурная схема скорректированной системы:

W_нс (Р) - передаточная функция нескорректированной системы;

W_ку (Р)  - передаточная функция корректирующего устройства.

Поскольку для последовательного соединения

W_ск(P)=W_ку(P) ^.W_нс(P)                                            (5)

или

L_ск=L_ку -L_нс ,                                                           (6)

то

L_ку= L_ск -L_нс .                                                            (7)

Таким образом, для определения ЛАХ последовательного корректирующего устройства необходимо:

- построить ЛАХ L_нснескорректированной (исходной) системы;

- построить желаемую ЛАХ L_ж;

- найти ЛАХ L_кукорректирующего устройства, для чего из ЛАХ вычесть ЛАХ L_нс;

- по найденной ЛАХ L_куи таблицам характеристик типовых корректирующих устройств (табл. I, 2) определить схему и параметры коррекции.

Пример I. Передаточная функция системы имеет вид:

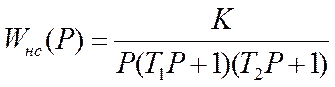
Определить схему и параметры последовательного электрического корректирующего устройства, если

K=80 c;    Т₁=0,2 с;     Т₂=0,02 с;   Т_пл=2 с;   

Структурная схема скорректированной системы изображена на рис. 7.

                      Рис. 7. Структурная схема скорректированной системы

Решение.

1. Строим ЛАХ нескорректированной системы. Частоты сопряжения равны:

       

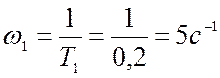
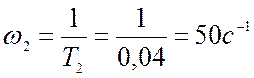
При =1 откладывается значение 20lgK=20lg80=38 дб.

Через точку А (рис. 8) проводим асимптоту с наклоном - 20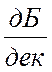  поскольку исходная система астатическая . При частотах сопряжения  и происходит излом L_нс на 20.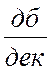

2. Определяем частоту среза желаемой ЛАХ L_ж.

Нижняя граница

                                ,

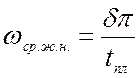где =4,3 (см. рис 1).

Следовательно ,

                             

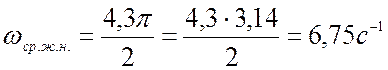
3. Определяем запасы устойчивости по модулю h и по фазе , исходя из перерегулирования  (рис. 3):

                            h=13 дб;          =42⁰ .                 

 

 

 

 

 

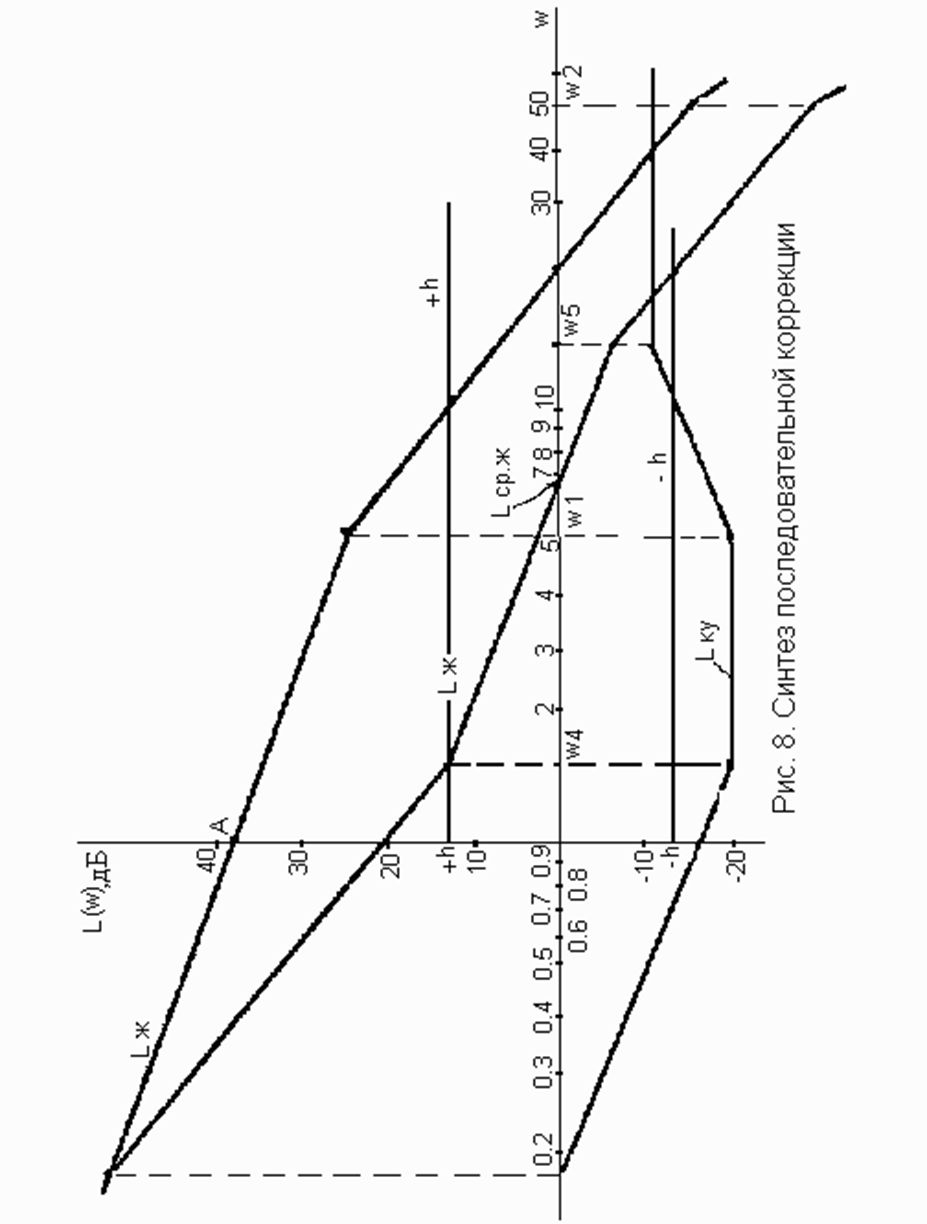
4. Строим желаемую ЛАХ.

При ω_ср.ж проводим асимптоту с наклоном – 20 дБ/дек. Отложим по оси ординат запас устойчивости по модулю ±h и проведем линии, параллельные оси частот ω. Точки пересечения прямых +h и –h с асимптотой – 20 дБ/дек определяют среднечастотную зону.

Для упрощения корректирующего устройства произведем излом высокочастотного участка L_ж в точке ω₅ , уменьшив при этом запас по модулю до 9 дБ. Однако в области высоких частот некоторое уменьшение запаса устойчивости обычно несущественно ухудшает переходный процесс, поскольку при этом увеличение абсолютного значения | P_min | по сравнению с принятым | P_min |=P_max – 1 незначительно. По виду L_ку определяем электрическую схему корректирующего устройства (рис. 9).

               

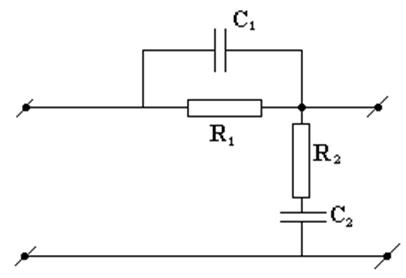
                         Рис. 9. Схема коррекции

Передаточная функция коррекции равна:

  ,

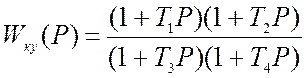где T₁=R₁C₁;   T₂=R₂C₂ ;

T₃ и Т₄ определяются из системы уравнений

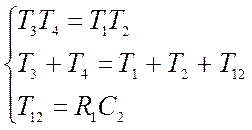
Для рассмотренного примера:

          

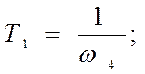
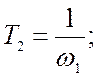
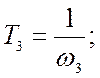
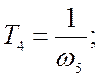
Определение параметров элементов корректирующего устройства является неоднозначной задачей, поскольку алгебраическая система, связывающая неизвестные параметры корректирующего устройства с коэффициентами его передаточной функции является избыточной, т.е. число неизвестных  превышает число уравнений. Поэтому при расчете элементов схемы корректирующего устройства одним из её параметров задаются            ( обычно задаются величиной емкости С₂ из условия согласования входного и выходного сопротивлений ).

Определим запас по фазе при частоте среза

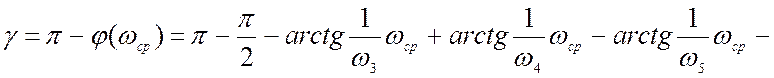
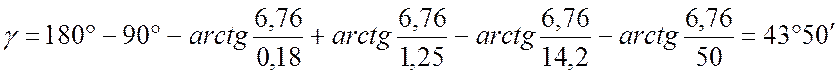
Синтез параллельных корректирующих

устройств пот ЛАХ