В автосчислителе выработанные величины Dj и Dl автоматически складываются с координатами исходного счислимого места (рис. 3.10).
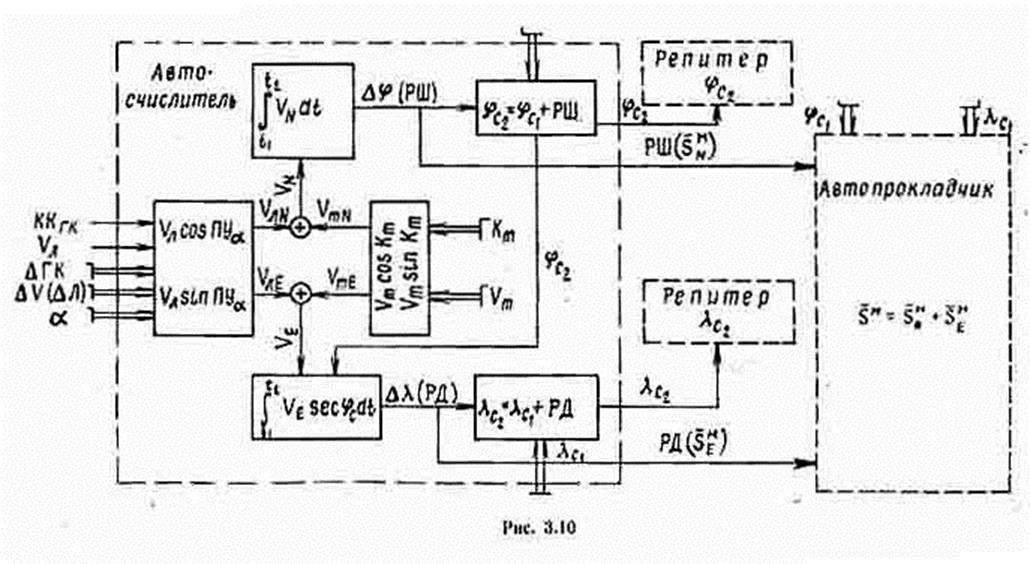
Входными величинами автосчислителя являются независимые переменные ККГк, Vл (вводятся автоматически от гирокомпаса и лага), DГК, Dл, a, Кт, Vт, jc и lc (вводятся вручную).
Графическое счисление на планшете автопрокладчика осуществляется построением вектора Sм = SмN + +SмE по составляющим Djм и Dlм, выраженным в текущем масштабе карты.
В современных условиях автоматическое аналитическое счисление реализуется в аналоговых вычислительных машинах автопрокладчиков и автосчислителей и в электронных цифровых вычислительных машинах ИНС.
Накопление погрешности в счислимом месте с течением времени обусловливает необходимость периодической его корректуры. Корректура счислимого места производится путем определения места корабля по измерениям, выполняемым относительно навигационных ориентиров с известными координатами.
В качестве навигационных ориентиров используются наземные и небесные объекты. К наземным ориентирам относятся маяки, радиомаяки, знаки, вершины гор, рельеф дна, приметные искусственные сооружения (башни, трубы и т. п.), специальные радиотехнические станции и т.д., к небесным ориентирам относятся естественные светила: солнце, звезды и планеты.
Соответственно этому все способы определения места по наземным ориентирам называют навигационными, а по небесным ориентирам - астронавигационными. Основой определения места является измерение навигационных параметров, зависящих от взаимного расположения корабля и ориентира. Навигационный параметр зависит от положения наблюдателя относительно ориентира и является функцией географических координат места наблюдателя. Поэтому каждый навигационный параметр можно представить в виде известной функции
U = f (j, l).
Эта функция выражает собой уравнение навигационной изолинии.
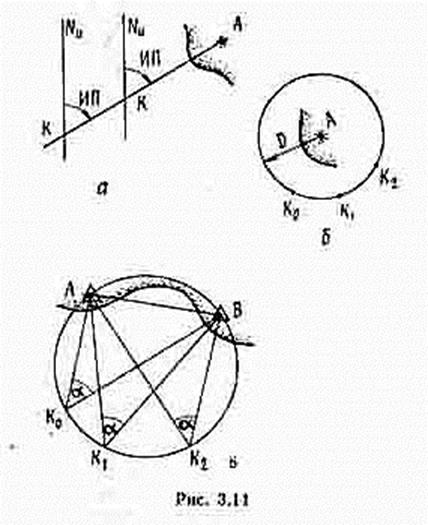
Навигационная изолиния - линия на земной поверхности, каждая точка которой соответствует одному и тому же значению навигационного параметра. Так, при измерении пеленга на ориентир А (рис. 3.11,а) изолинией является линия истинного пеленга (изоазимута), при измерении дистанции-изостадия (окружность) , радиус которой равен измеренной дистанции D (рис. 3.11,6), при измерении горизонтального угла a между ориентирами А и В - изогона, то есть дуга окружности АКB (рис. З.11 в), вмещающая угол a, опирающийся на хорду АВ, и т. д.
Если же одновременно измерить навигационные параметры U1 и U2 относительно двух ориентиров, то соответствующие функции составят систему из двух уравнений с двумя неизвестными j и l:
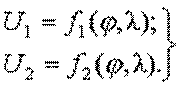
Cовместное решение уравнений этой системы дает искомые координаты корабля j и l.
С геометрической точки зрения нахождение обсервованного места корабля сводится к проведению на карте двух навигационных изолиний U1 и U2 и к определению точки их пересечения (рис. 3.12).
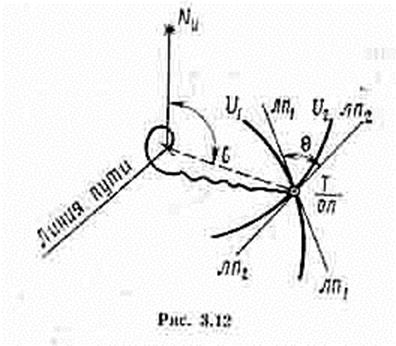
При определении места корабля по измеренным навигационным параметрам в большинстве случаев сами изолинии не строятся. На кратчайшем расстоянии от счислимого места прокладываются их небольшие отрезки в виде прямых линий, касательных к данным изолиниям. Эти прямые называются линиями положения.
Точка пересечения линий положения на карте называется обсервованным местом (обозначается значком Q), а координаты- обсервованными координатами j0 и l0.
Счислимое место из-за погрешностей в элементах счисления в общем случае не совпадает с обсервованным. Разница между обсервованным и счислимым местами называется невязкой. Она характеризуется направлением со счислимого места к обсервованному и длиной отрезка между этими местами в милях. Например, (рис. 3.12) С = 105°-1,2 мили. Невязка обозначается символом С и графически изображается затухающей кривой от счислимого места к обсервованному, пересекая при этом линию пути. Время и отсчет лага указываются у обсервованного места. За исходную точку для дальнейшего счисления принимается данная обсервация.
Вследствие того что измеренные навигационные параметры содержат некоторые погрешности (инструментальные, графических построений, несовершенство органов чувств наблюдателя и т. п.), место, полученное по ним, будет также определено с некоторой погрешностью. В зависимости от происхождения погрешности измерений бывают систематические и случайные.
Систематические погрешности - это постоянные погрешности, возникающие вследствие неточного значения поправок приборов и инструментов.
Случайные погрешности происходят главным образом от несовершенства органов чувств человека, случайных внешних причин и т. д. Величина погрешности лежит в определенных пределах. Случайные погрешности, хотя и неизбежны, всегда подчиняются какому-либо общему закону. Зная этот закон, их можно учитывать.
Для оценки точности измерений навигационного параметра применяется средняя квадратическая погрешность измерения, которая наиболее точно отражает качество измерений и выражается формулой
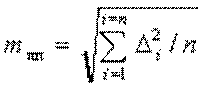
где Di -погрешность измерения, равная разности истинного и измеренного значения данной величины; n - количество измерений.
Средняя квадратическая погрешность измерений определяется из наблюдений.
Чтобы оценить точность обсервованного места, используется радиальная средняя квадратическая погрешность М0 места, представляющая собой радиус круга, в пределах которого находится вероятнейшее место корабля (с вероятностью 68,3%).
При определении места по двум линиям положения
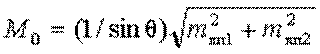(3.11)
В этой формуле mлп1 и mлп2 - смещения линий положения, соответствующие средним квадратическим погрешностям измерения навигационных параметров, используемых для определения места; q - угол пересечения линий положения.
Анализ формулы (3.11) показывает, что величина радиальной погрешности зависит не только от погрешностей измерений, но и от угла пересечения линий положения. При прочих равных условиях наблюдения М0 будет наименьшая, когда q = 90°. Поэтому в практике необходимо подбирать такие ориентиры, линии положения которых пересекались бы под углом, близким к 90°, во всяком случае под углом не меньше 30 и не больше 150°.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.