Технологические зависимости и показатели эффективности бурения резанием, страница 4

             Зная величину  (по первым измерениям), по формуле (3.31), подставляя в нее опытные значения t и соответствующие им величины , можно получить ряд значений t₀, из которых необходимо взять среднее.

             Нами и Е.Д. Карпухиным в различных условиях получено хорошее совпадение расчетных и фактических данных. Для кривых бурения с наклонной асимтотой, отражаемых формулой (3.23) и графиком  (рис. 3.4), также применим графо-аналитический метод определения параметров формулы.

             В связи с тем, что формулы (3.19) и (3.23) имеют не два, а три постоянных параметра, t_o находится описанным выше приемом. Затем уравнение (3.23) преобразуется к виду:

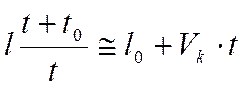                                        .                               (3.32)

 В левую часть уравнения (3.31) входят известные  величины, а в правую – линейная функция от t. В системе координат t и 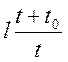 получается сглаживающая прямая линия (рис. 3.6), наклонная ордината которой будет l₀, а угловой коэффициент V_к.

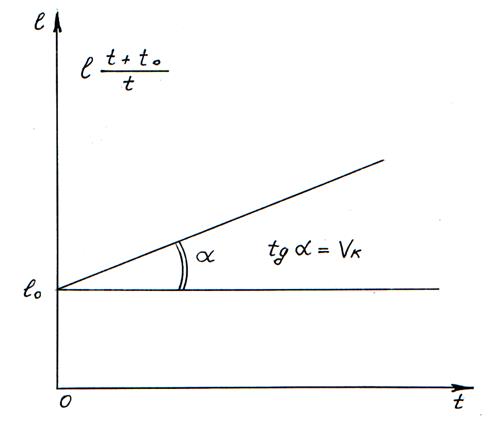
Рис. 3.6. Спрямление зависимости  (t), выраженной формулой (3.23)

             Параметры V₀, V_k, t₀, ₀ формулы (3.24) по опытным данным можно определить, не прибегая к графическому построению, расчетным путем. Приближенное значение V₀ в начале бурения для первой точки, когда долото имеет новое, не изношенное вооружение, равно  Приближенное значение V_k можно получить по двум последним замерам [41].

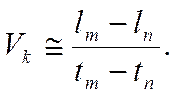                                                                    (3.33)

Преобразовав (3.24) к виду:

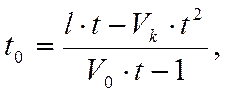                                                                          (3.34)

и подставляя в него значения V₀ и V_k, а также значения  опытных данных  и t для ряда точек кривой (t), получим ряд значений  t₀, из которых берется среднее.

             Несколько иной, но достаточно точный приближенный способ определения по опытным данным значений постоянных величин в формуле бурения (3.23) дается М.М. Протодьяконовым (младшим), который приводит уравнение (3.23) к виду:

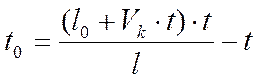                                       .                                (3.35)

             Анализ целого ряда конкретных случаев показывает, что при малых значениях времени бурения t величина V_k·_.t  составляет 1 – 5 % от величины ₀. Поэтому с достаточной для практики точностью приближенно можно принять:

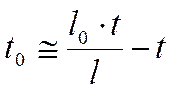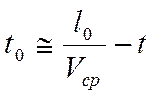                         или     .                       (3.36)

             Беря две точки в начальной  части кривой t₁, ₁; t₂, ₂ непосредственно из опытных данных и подставляя их в последнее уравнение (3.36), получаем два уравнения, из которых находим величину t₀:

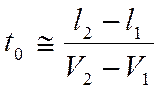                                            .                                       (3.37)

Найденная величина t₀ подставляется в исходное уравнение (3.23), которое дальше решается уже не только для малых значений t, но и для любых практических величин времени бурения. Если теперь в то же уравнение (3.23) подставить еще значения  координат двух опытных точек (желательно в начале и в конце кривой), то можно получить два уравнения с двумя неизвестными  пока постоянными параметрами. Путем решения этих уравнений получаются следующие выражения:

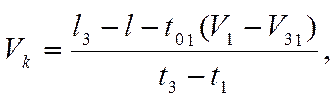                                           (3.38)

                                                (3.39)

          Можно видеть, что получились несложные формулы для  определения постоянных параметров кривой бурения. Подставляя в них значения координат трех точек, взятые из опыта, можно быстро и просто найти величины искомых  параметров.

          Учитывая, что опытные точки всегда имеют некоторый разброс, рекомендуется взять не одну, а две или три группы из трех точек и, найдя для каждой группы значения постоянных параметров, взять из них среднеарифметическое. Тогда эмпирическая кривая пройдет между всеми точками с максимальным отклонением от них.

          Естественно, кривые (t) должны фиксироваться на буровом станке при постоянных режимных параметрах и в однородных породах. В то же время, фиксируя (t) при разных режимах бурения и горных породах, можно получить зависимости, позволяющие определить рациональные режимы бурения для различных горных пород. Однако такие эксперименты весьма трудоемки, требуют специальной аппаратуры. Для установления  рациональных режимов целесообразнее пользоваться двухкоординатными приборами, записывающими функции V(Р), V(n) и другие при ступенчатом изменении характеристик горных пород.

Сопряжение таких приборов с компьютерной базой позволяет иметь методику достаточно быстрого установления оптимальных режимов бурения. Управление режимом бурения  может осуществляться различными методами, в том числе  по программным зависимостям (моделям), устанавливаемым на основе  статистических данных.

          Вернемся к дальнейшему анализу кривых бурения. Входящий в уравнения этих кривых параметр  t₀ (постоянная времени бурения), определяемый делением максимальной стойкости  долота   на начальную скорость бурения V₀, является весьма информативным.

          Из уравнения (3.28) следует, что мгновенная текущая скорость бурения:

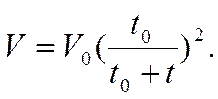                                                             (3.40)

          Согласно выражению (3.26) средняя скорость бурения:

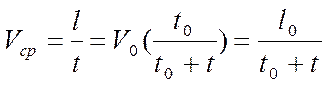                            .                (3.41)

          Отношение этих скоростей составит:

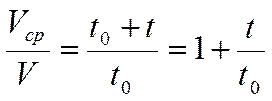                                 .                   (3.42)

          Из уравнений (3.40) – (3.42) нетрудно установить связь  между текущей, начальной и средней скоростью бурения:

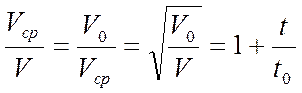                                 .               (3.43)

          Полученная взаимосвязь скоростей бурения, отмеченная и в работе [42], позволяет полнее анализировать результаты промышленного бурения, но она получена без учета оптимального времени пребывания долота на забое.

          Оптимальное время бурения t_опт затупляющимся долотом того или иного типа иногда устанавливают по максимуму рейсовой скорости для условий бурения однородной породы  при постоянстве режимных параметров. Для определения V_{p max}  находят первую производную выражения  (3.2) и приравнивают ее к нулю:

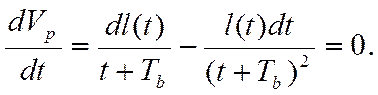
Откуда получают: