Технологические зависимости и показатели эффективности бурения резанием, страница 3

             Построение этого уравнения  по опытным данным выполняют искусственным спрямлением зависимости с помощью двойной логарифмической сетки. Показатель степени в полученном уравнении параболы обычно получается  дробным и формула эта не имеет правильной размерности и физического смысла. Вычисления достаточно трудоемки.

             Наиболее удобное для практического применения уравнение кривых бурения предложено М.М. Протодьяконовым (младшим) [39]; его метод принимается за основу. Графическое представление кривой бурения показано на рис. 3.4.

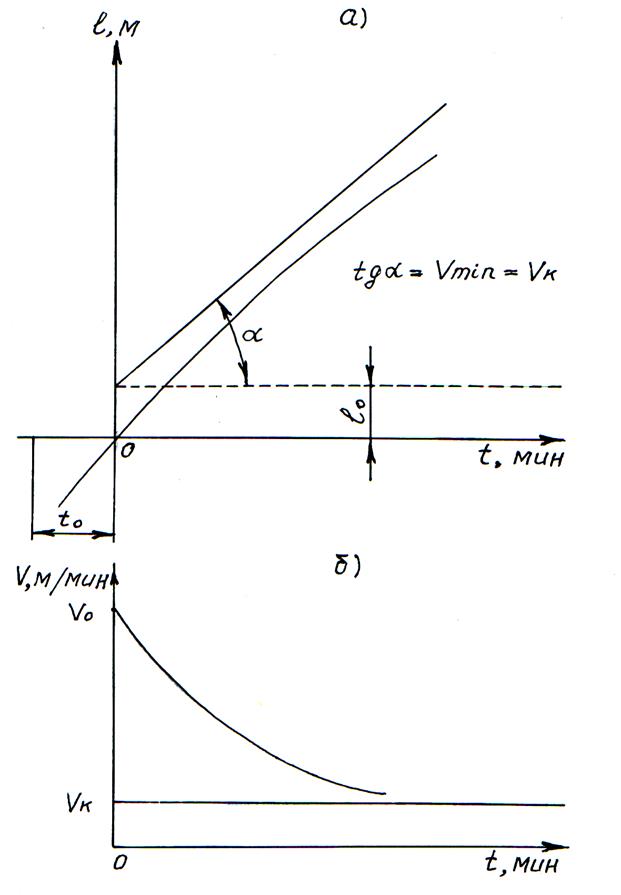
Рис. 3.4. Кривая бурения (а) и изменение скорости бурения

 по времени (б)

             По своему характеру кривая бурения имеет наклонную асимтоту (а при сильном затупляющемся буровом инструменте – горизонтальную асимтоту). Тангенс угла этой асимтоты представляет собой минимальную скорость бурения V_min, к которой будет стремиться текущая скорость бурения по мере затупления долота. Уравнение этой асимтоты следующее:

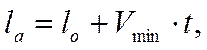                                          м,                           (3.18)

где l_o – ордината асимтоты, м; V_min – минимальная или конечная (V_к) скорость бурения, м/мин.

             При t = 0 должно быть = 0; при больших значениях времени  уравнение кривой совпадает с уравнением асимтоты: = _a.

Исходя из принятых представлений, уравнение кривой бурения представляет собой уравнение смещенной гиперболы следующего вида:

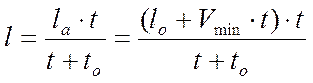                                    .                             (3.19)

             Для получения уравнения (3.19), рекомендованного М.М. Протодъяконовым (младшим), необходимо находить значения трех постоянных величин для каждых условий опыта: l_o, t_o, V_min, вместо двух величин для параболической зависимости. Введение дополнительной постоянной позволяет получить  лучшую сходимость эмпирической кривой и опытных данных. Важным преимуществом формулы (3.19) является также совпадение размерности левой и правой частей уравнения и отсутствие в ней дробных показателей.

             Согласно формуле (3.19) средняя скорость за чистое время бурения составляет:

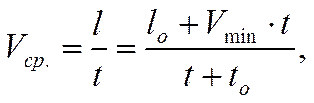                                                   (3.20)

откуда начальная скорость бурения (t = 0) ,будет:

                                                                          (3.21)

При  из той же формулы (5.19) находится величина конечной скорости  бурения:

                                                                           (3.22)

             Физический смысл величин, входящих в (3.19), трактуется следующим образом. Величина l_o представляет собой глубину скважины, которую можно было бы пробурить нетупящимся долотом, т.е. с постоянной начальной скоростью V_o за  время t_o. Величину  t_o   М.М. Протодьяконов (младший) назвал «постоянной времени бурения». Если подставить в уравнение (3.20) значение t = t_o, то получим: 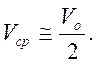 Отсюда следует, что параметр t_o представляет собой время, в течение которого начальная скорость уменьшается вдвое. Величина  V_min, как это вытекает из (3.22), представляет собой конечную скорость бурения при полностью затупленном долоте. Поэтому формула (3.19) может быть представлена в виде:

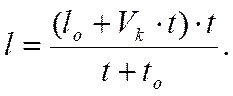                                                                   (3.23)

             Из выражения (3.21) следует, что . Подставляя это значение  в формулу (3.23), получим

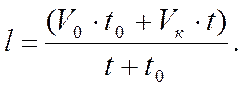                                                                  (3.24)

             Формула (3.24) удобна для приближенных расчетов, т.к. начальная и конечная скорости бурения легко определяются на действующем станке. Формулы (3.19) и (3.23) могут иметь частные виды. При сильно затупляющихся долотах, например, при бурении режущими долотами типа ДР и ДЗДШ в крепких породах () конечная скорость может быть равной нулю (V_k = 0). Тогда формулы (3.23)  и  (3.24) приобретают виды:

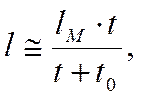                                                                                  (3.25)

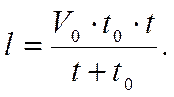                                                                             (3.26)

В этом случае в формуле (3.25)  представляет собой теоретическую максимальную (определяемую расчетным путем) стойкость (ресурс) долота по вооружению, а t₀ – время, которое потребовалось бы  для проходки, равной максимальной стойкости долота, если бы  начальная скорость  бурения оставалась неизменной, т.е. . Параметр  отличается от технической стойкости долота , определяемой долговечностью элементов долота или по конечной скорости бурения.

             Важно отметить, что параметры _0,  и t_o характеризуют не только конструкцию долота, но и условия его отработки – свойства пород и режим бурения.

Из уравнения (3.25) получаем выражение скорости бурения в зависимости от времени:

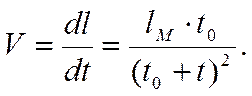                                                      (3.27)

Учитывая, что , имеем:

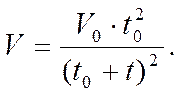                                                                 (3.28)

             Формулы (3.27) и (3.28) отражают изменение текущей скорости бурения вследствие непрерывного изнашивания бурового долота.

Для определения параметров  и t_o кривой бурения по формуле (3.25), по опытным данным уравнение (5.25) приводится к линейному виду:

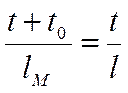                                         .                              (3.29)

Тогда при постоянных значениях  и t_o левая часть уравнения (3.29) представляет собой линейную функцию от t. Величина, стоящая в правой части, может быть вычислена для взятых из опыта значений   и t. Следовательно, в системе координат t и t/ уравнение (3.25) изображается прямой линией (рис. 3.5), которая отсекает на отрицательной оси абсцисс отрезок t_o и имеет угловой коэффициент .

             Параметры  и t_o могут определяться из опытных данных не только графическим способом и с помощью формул [39, 40]. Уравнение (3.26) приводится к виду:

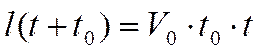                                   .                                    (3.30)

 

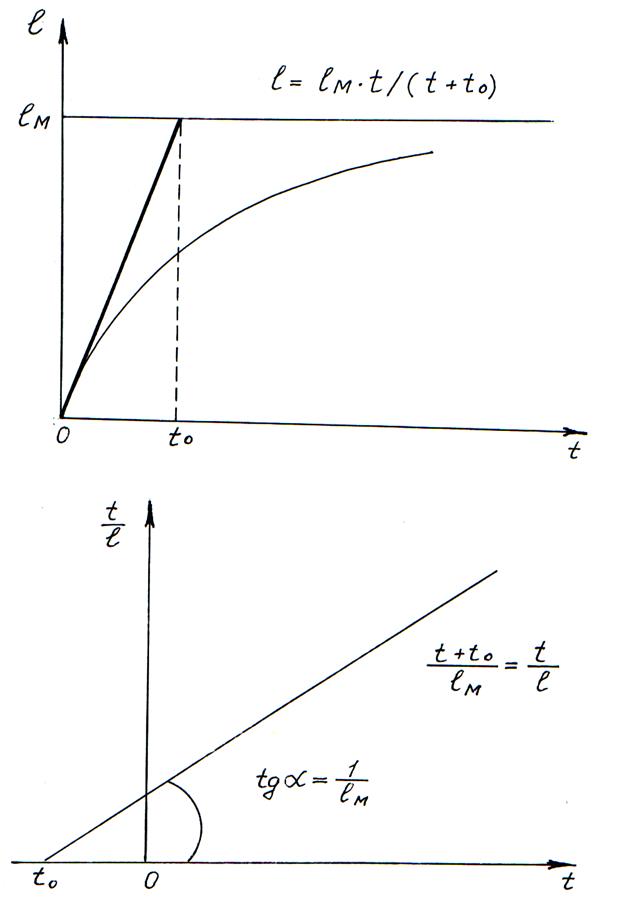
Рис. 3.5. Спрямление зависимости проходки на долото  от времени

бурения t

Из уравнения (3.30) находится:

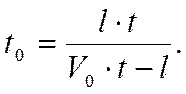                                                                        (3.31)