где Н – проходка долота, м; Vо – начальная скорость бурения, м/мин; ко – коэффициент, характеризующий темп падения скорости бурения во времени и определяемый экспериментально в зависимости от параметров режима бурения, конструкции долота, коэффициента трения и многих других факторов.
Б.Н. Кутузов [37] использовал для функции V(t) эллиптический закон (применительно к шарошечному бурению):
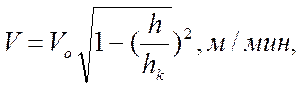(3.12)
где Vo – начальная скорость бурения новым долотом, м/мин; h – текущая суммарная глубина проходки долотом, м; hk – максимальная суммарная глубина проходки (максимальная стойкость долота), м.
Предложено еще не менее
десятка формул для функций 
(t) и V(t), как правило,
степенных с трудно определяемыми коэффициентами.
Для проектирования и
совершенствования технологии бурения в условиях действующих карьеров наиболее
приемлем простой метод (способ) определения зависимости V(t) по графику изменения проходки во
времени. Функцию (t) часто называют кривой проходки или кривой бурения. Ее график
можно легко построить путем хронометражных наблюдений или с помощью несложного
прибора ПАЗС непосредственно на действующем буровом станке в условиях карьера.
В зависимости от типа и
конструкции бурового инструмента, его износостойкости, свойств буримых пород и
параметров режима бурения вид функции 
может
быть криволинейным (рис.3.1) для затупляющихся долот или практически линейным
(рис.3.2) для самозатачивающихся режущих долот и некоторых типов медленно затупляющихся
штыревых ШД, выходящих из строя по опоре.
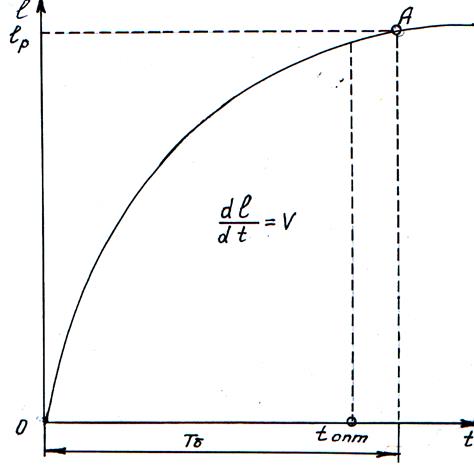
Рис. 3.1. Кривая бурения затупляющимся долотом: – текущая длина (проходка) скважин,
м; p -
проходка за рейс, м; Тб – продолжительность чистого бурения за рейс,
мин; tопт
– оптимальное время работы долота, мин; А – момент полного отказа долота
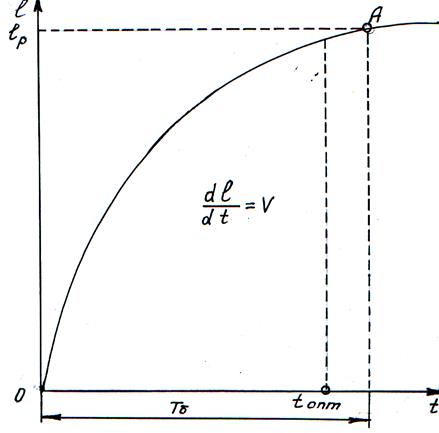
Рис. 3.2. Кривая бурения самозатачивающимся или медленно затупляющимся долотом, например, шарошечным типа ОК в породах средней крепости при отказе по опоре
На рис. 3.1 и 3.2 кривые
(t) представлены в пределах рейса долота, на оси абсцисс
отложено время чистого бурения, а на оси ординат - соответствующая проходка.
Долота могут быть отработаны до отказа, например, при заклинивании опоры ШД
(рис. 3.2 точка А) или до полного износа вооружения, когда скорость бурения
близка к нулю (рис. 3.1 точка А). Долото может заменяться при некотором
оптимальном времени бурения tопт по критерию минимальных удельных
затрат на бурение 1 м скважины или иному критерию.
Важность кривой бурения состоит в том, что она наглядно отражает характер изменения текущих значений скорости бурения и проходки в соответствии с выражениями (3.3) и (3.4).
В глубоком бурении [38], где большую долю рабочего времени занимают спуско-подъемные операции, используют кривые проходки (рис. 3.3) вида L = α(β), где L – глубина скважины; β – порядковый номер рейса.
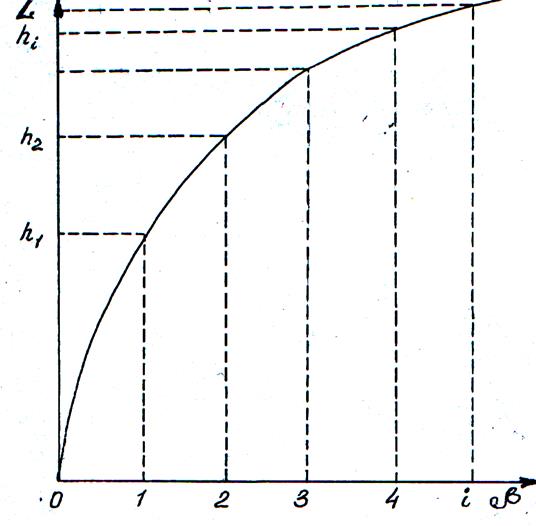
Рис. 3.3. Кривая (график) проходки глубокой скважины
По уравнениям этих кривых определяют объем и продолжительность спуско-подъемных операций, нормируют расход долот, устанавливают рациональные режимы бурения. С каждым рейсом достигнутая глубина скважины уменьшается даже при постоянной стойкости заменяемых долот вследствие роста потерь времени на спуско-подъемные операции.
Проходка за рейс связана с глубиной скважины зависимостью:
,
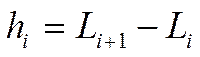где Li – глубина скважины в начале бурения после спуска долота на забой; Li+1 – глубина скважины (после отработки долота) к началу извлечения инструмента из скважины.
В глубоком бурении текущая проходка за рейс долота hi с глубиной уменьшается по многим причинам (увеличение потерь времени на спускоподъемные операции, рост горного и гидростатического давлений, ухудшение условий очистки забоя и т.д.). Номера рейсов β на оси абсцисс (рис. 3.3) располагаются с равным интервалом, что равносильно равным промежуткам времени. Поэтому характер изменения кривых проходки L(β) глубоких скважин в общем виде сходен с кривыми бурения взрывных скважин.
Применительно к глубокому бурению установлены следующие виды кривых проходки и их уравнения:
1. Прямолинейный тип кривой с уравнениями
и 
,
(3.13)
где L – глубина скважины; β – число рейсов; α и 
– коэффициенты, причем α > 1 и > 1.
Такой вид кривой встречается при бурении сравнительно неглубоких скважин.
2. Параболический тип кривой с уравнением
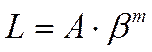, (3.14)
где А – коэффициент, А > 1; m – показатель степени, m < 1 (0,2 < m < 0,7).
3. Гиперболический тип кривой с уравнением
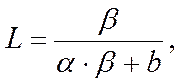(3.15)
где α и – коэффициенты,
величина которых меньше 1.
В отличие от глубокого бурения, где фактор глубины весьма значим, на карьерах картина бурового процесса принципиально иная. В подавляющем большинстве случаев глубина взрывных скважин составляет 12 – 16 м, реже до 50 – 60 м, и при пневматической и шнеко-пневматической очистке скважин в гораздо меньшей степени влияет на скорость бурения. Проходка на долото на большинстве карьеров в несколько раз превышает глубину скважины (lp >> Lскв) , поэтому можно говорить о суммарной глубине нескольких мелких скважин, приходящихся на один рейс долота:
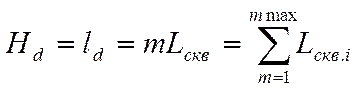, (3.16)
где Hd – проходка на долото, м; 
– стойкость долота, м; m – число скважин, приходящихся на
рейс долота; Lскв. – глубина взрывной скважины, м.
В области бурения
взрывных шпуров и скважин функцию (t) чаще всего выражают эмпирическим
уравнением в показательной формуле:
. (3.17)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.