Работа с процессорами Word и Excel при создании технических текстов. Однофакторная модель прогноза уровня спроса на выпускаемую продукцию: Методические указания к лабораторным работам, страница 7

	I	J	K	L	M	N	O	P
17		Ym(t)=B0+B1*t+B2*t^2+B3*t^3
18	t	B0	B1*t	B2*t^2	B3*t^3	Ym(t)		(Ym-Y)^2
19	1	10,839	-0,2611	0,1259	-0,0051	10,0436	0,00436	0,001901
20	2	10,1839	-0,5222	0,5036	-0,0408	10,1245	0,00740	0,0057002
21	3	10,1839	-0,7833	1,1331	-0,1377	10,396	0,00038	1,6E-05
22	4	10,1839	-1,0444	2,0144	-0,3284	10,8275	0,00254	0,0007582
23	5	10,1839	-1,3055	3,1475	-0,6375	11,3884	0,001017	0,0001346
24	6	10,1839	-1,5866	4,5324	-1,1016	12,0481	0,004008	0,0023136
25	7	10,1839	-1,8277	6,1691	-1,7493	12,776	0,001875	0,000576
26	8	10,1839	-2,0888	8,0576	-2,6112	13,5415	0,004301	0,0034223
27	9	10,1839	-2,3499	10,1979	-3,7179	14,314	0,000979	0,000196
28	10	10,1839	-2,611	12,59	-5,1	15,06	0,002458	0,0013784
29	11	10,1839	-2,8721	15,2339	-6,7881	15,7576	0,002683	0,0017978
30	12	10,1839	-3,1332	18,1296	-8,8128	16,3675	0,001981	0,0010562
31	13	10,1839	-3,3943	21,2771	-11,204	16,862	0,033996	0,0192463
32	14	10,1839	-3,8554	24,8784	-13,994	17,2105	0,283303
33	15	10,1839	-3,9185	28,3275	-17,212	17,3824		0,0017497
34	16	10,1839	-4,1776	32,2304	-20,889	17,3471	Sy=0,041829

Использование окна Макрос

1.  Выполнить команду Сервис/Макрос/Макросы. Откроется диалоговое окно.

2.  Выбрать имя макроса Гаусс и нажать кнопку Выполнить.

В результате выполнения макроса Гаусс в ячейки A25:D28 будут импортированы значения элементов треугольной матрицы, а в ячейки Н25:Н28 – значения коэффициентов регрессионной модели: b₀=10,184; b=-0,2611; b₂=0,1259; b₃=-0,0051. После подстановки этих значений коэффициентов в уравнение (7) регрессионная модель для ряда, заданного табл. 1, примет вид

Y_m(t)= 10.184 - 0.2611t + 0.1259t² - 0.0051t³ .                                    (10)

Реализация третьей операции требует вычисления значений y_m(t_i) в точках наблюдения t_i=1,2,…,12 и за пределами интервала наблюдения при t=13,14,15. Результаты вычислений значений слагаемых регрессионной модели и y_m(t) размещены в ячейках I19:M34 и показаны в табл. 5.

Для выполнения четвертой операции по вычислению величин S_y и e по формулам (5) и (6) в ячейки О19 и Р19 введем формулы:

=ABS((N19-H3)/H3), (11)

=(N19-H3)^2.                                                  (12)

Далее, распространив подобные формулы на ячейки О19:О33 и Р19:Р33, получим 15 значений элементов каждого ряда. Затем, осуществив суммирование, вычислим значения S_y и e, которые поместим в ячейки О34 и Р34.

Воспользовавшись данными фактического объема продаж y(t_i) (ячейки Н3:Н14), данными модели y_m(t_i) (ячейки N19:N34), значениями моментов времени t_i (ячейки I19:I34) и кнопкой Мастер диаграмм на стандартной панели, получим графики этих функций. Эти графики будут воспроизведены, если нажать клавишу Ctrl и, не отпуская ее, с помощью левой клавиши мыши выделить содержимое столбцов H, I и N, а затем щелкнуть по кнопке Мастер диаграмм на стандартной панели инструментов. После выполнения четырех шагов Мастера диаграмм на экране появятся графики ,  и , позволяющие качественно оценить точность аппроксимации. Далее следует проверить модель на адекватность (см. лаб. раб. № 3).

Этой операцией заканчивается реализация получения регрессионной полиномиальной модели .

В экспоненциальной модели 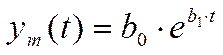 требуется определить значения коэффициентов  и . Это возможно тогда, когда известны значения ординат 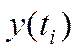 реального процесса в моменты времени , i=1, 2, …, n. Уравнение (4) является нелинейным.

Вычисления по определению   и  упрощаются, если применить операцию логарифмирования к 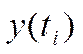 и . Тогда уравнение (4) и квадратический критерий примут вид:

                                          

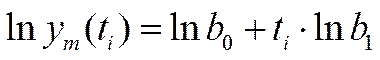
,                                                       (13)

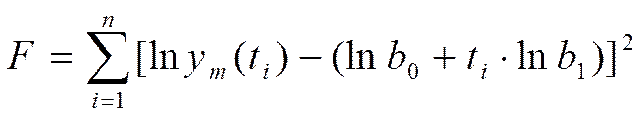.                          (14)

                                                                                                                                                                                                Как и ранее, условием минимума F является равенство нулю производных:

,

.

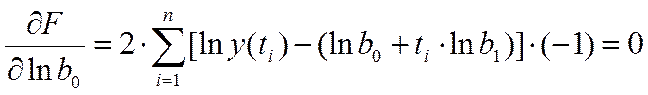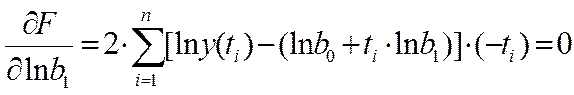Перепишем эту систему из двух уравнений в виде

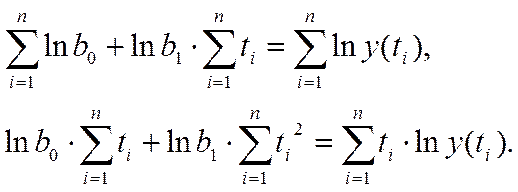                                 (15)

Значения моментов времени  и  известны. Поэтому значения сумм, входящих в эти уравнения, легко вычислить на предварительном этапе.

Обозначим , , , .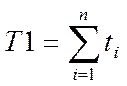

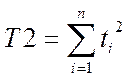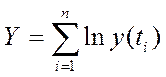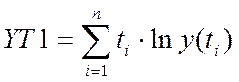Подставим конкретные значения этих сумм в (15). В результате получим:

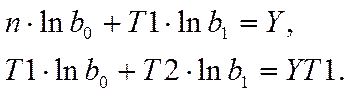                                       (16)

Из решения этой системы следует:

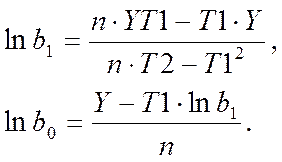                                           (17)

По таблице натуральных логарифмов находим значения коэффициентов экспоненциальной модели  и .

Порядок выполнения работы

1.  Полностью воспроизвести пример, приведенный в настоящем описании для полиномиальной модели третьего порядка [формула (7)] с выводом исходных данных y(t_i; i=1,2,…,12) и значений модели y_m(t_i; i=1,2,…,15) на диаграмму.

2.  Выбрать место для таблицы, структура которой показана далее, сформировать эту таблицу и заполнить ее данными.

Экспоненциальная модель