Работа с процессорами Word и Excel при создании технических текстов. Однофакторная модель прогноза уровня спроса на выпускаемую продукцию: Методические указания к лабораторным работам, страница 5

Для получения значений коэффициентов модели при известных базисных функциях j_j(t) применяют обычные методы математического анализа. Условием минимума критерия F является

.

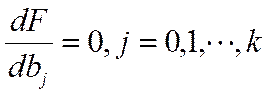В экономико-математических исследованиях наибольшее применение получили следующие виды однофакторных моделей:

линейная     y_m(t) = b₀ + b₁t;                                                                         (2)

полиномиальная   y_m(t) = b₀ + b₁t + b₂t² +…+ b_kt^k,  где j_j(t) = t^j;                (3)

экспоненциальная 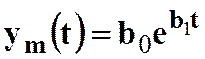     .                                                        (4)

Модель считается известной, если определены значения b_j. Полученную модель можно использовать для вычисления значений y_m(t), выходящих за пределы наблюдаемого периода T_н. При этом выдвигается гипотеза о том, что будущее является продолжением настоящего при сохранении стабильности существующих тенденций. Погрешность при составлении прогноза на будущее обычно оценивают величиной стандартного отклонения S_y в наблюдаемом периоде, определяемого по формуле

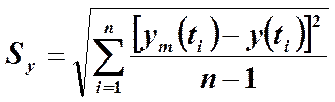.                                                                          (5)           

Считая, что ошибка прогнозирования подчиняется нормальному закону распределения, можно утверждать, что с вероятностью P=0,95 ожидаемое значение y_m(t) будет находиться в интервале (y_m(t)+2*S_y, y_m(t)-2*S_y). Величину относительной ошибки аппроксимации оценивают по формуле

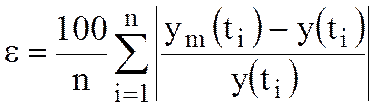%,                                                                (6)

где e - средняя относительная ошибка аппроксимации опытных данных сглаживающей кривой y_m(t). Обычно задаются допустимой ошибкой аппроксимации, не превышающей 10 %. Интервал прогноза выбирают порядка 20-30 % от длительности наблюдаемого периода Т_н. Прогнозируемые значения y_m(t) необходимо по истечении времени прогноза сравнивать с фактическими данными и, если возникает необходимость, производить корректировку прогнозирующей функции.

Выбор конкретного типа модели обусловлен характером экспериментальных данных за период Т_н либо последовательным увеличением степени полинома модели (3) до тех пор, пока относительная ошибка аппроксимацииe  станет меньше 5-10 %.

Пример применения табличного процессора Excel

Пусть предприятие выпускает некоторую продукцию. Объем продаж продукции за 12 предшествующих месяцев (наблюдаемый период Т_н) в тоннах показан в табл. 1.

                                                                                                    Таблица 1

I	1	2	3	4	5	6	7	8	9	10	11	12
ti	1	2	3	4	5	6	7	8	9	10	11	12
y(ti)	10	10,2	10,4	10,8	11,4	12	12,8	13,6	14,3	15,1	15,8	16,4

Для изучения выберем полиномиальную и экспоненциальную модели. Полиномиальная модель третьего порядка имеет вид

y_m(t) = b₀ + b₁t + b₂t² + b₃t³ .                                                                 (7)

Требуется найти значения коэффициентов b₀, b₁, b₂, b₃, доставляющих минимум функционалу

.

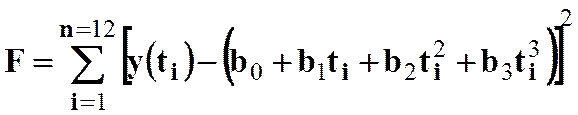Воспользовавшись методом наименьших квадратов, получим систему уравнений:

 ,

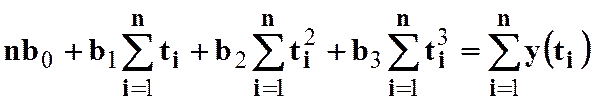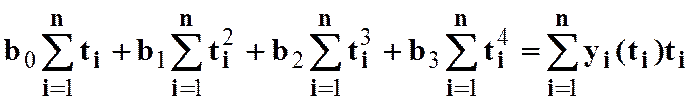,              (8)

,        

 .

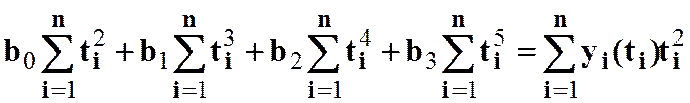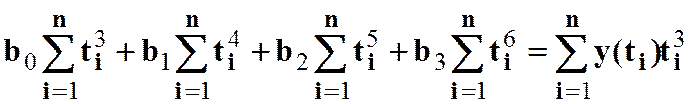
Все суммы, фигурирующие в данной системе уравнений, включают известные значения, могут быть вычислены заранее и рассматриваться как постоянные величины. Так как определяемые коэффициенты модели ,  и  имеют единичную степень, то данная система уравнений является линейной, а ее матричная форма имеет вид

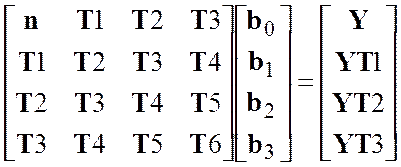 ,                                                           (9)

где Т1,Т2,…,Т6,Y,YT1,YT2,YT3 – значения сумм, фигурирующих в системе уравнений (8). Для решения данной системы уравнений выбран метод Гаусса, рассмотренный в лабораторной работе № 3.

Для получения прогнозирующей однофакторной модели требуются следующие операции.

1.  Привести систему уравнений (8) к матричному виду (9).

2.  Решить систему уравнений (9).

3.  По формуле (7) вычислить значения y_m(t_i) для t_i=1,2,…,15 и поместить их в таблицу.

4.  Вычислить величину стандартного отклонения S_y и оценку точности аппроксимации соответственно по формулам (5) и (6).

5.  Поместить график y(t_i) и график y_m(t_i) на одной диаграмме.

Выполнение этих операций хорошо вписывается в возможности табличного процессора Exсel. Отметим, что выполнение п. 2 требует применения макроса и приложения Visual Basic.

Для вычисления значений элементов временных рядов и соответствующих им сумм, входящих в систему уравнений (8), воспользуемся столбцами A, B, C ,D, E, F и H, I, J, K (см. табл. 2 и 3).         В ячейки второй строки введем их имена t, t^2, … , t^6 и y(t),                   y(t)*t,y(t )*t^2, y(t)*t^3. Так как n=12, то в строки с 3 по 14 столбцов А и Н занесем значения t₁, t_{2, …,} t₁₂ и y₁, y₂, …, y₁₂ из таблицы. Значение элементов остальных столбцов системы уравнений (8) являются производными от значений элементов столбцов А и Н. Для их вычисления в ячейку В3 введем формулу =А3*А3, в ячейку С3 - =В3*А3, в ячейку I3 - =Н3*А3, в ячейку J3 - =Н3*В3 и т.п. Распространим формулы строки 3 на строки 4,5,…,14. Для этого необходимы следующие операции: выделить  ячейки с А3 по F3, подвести курсор к правому нижнему углу ячейки F3, нажать левую клавишу мыши (курсор из белого “жирного” крестика превращается в “тощий” черный) и, не отпуская ее, тянуть за этот уголок до строки 14. Те же операции проделать и со столбцами H, I, J, K. В результате в соответствующих столбцах появятся значения элементов временных рядов. Значение суммы любого из указанных столбцов можно получить, нажав кнопку å на стандартной панели, и записать ее в соответствующий столбец строки 15 (табл. 2 и 3).

В ячейки А18:D18 введем текст “Исходная матрица уравнений”. Для удобства выполнения операции 1 сгруппируем полученные значения сумм столбцов в одном месте, а именно в ячейках А19:D22 и F19:F22. В ячейку Е22 введем число 3, соответствующее четырем уравнениям системы (9)  (табл. 4).

                                                                                                            Таблица 2