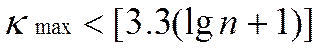 ;
(2)
;
(2)
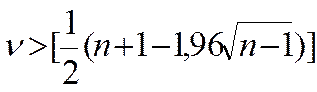 ,
(3)
,
(3)
где квадратные скобки означают целую часть. Правые части неравенств соответственно равны 6 и 3. Следовательно, гипотеза о случайности колебаний уровней εt с доверительной вероятностью 0,95 подтверждается.
Проверку соответствия распределения последовательности остатков εt нормальному закону распределения осуществляют с помощью показателей асимметрии (γ1) и эксцесса (γ2) по формулам:
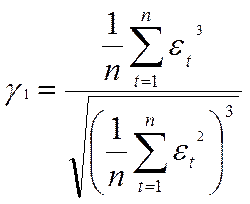 ;
(4)
;
(4) 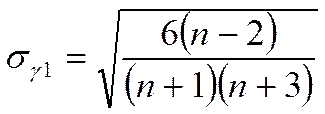 ;
(5)
;
(5)
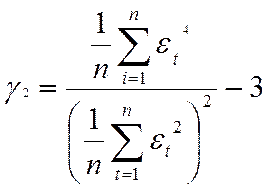 ;
(6)
;
(6) 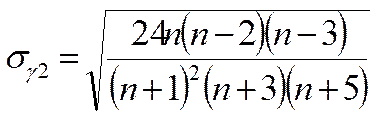 ;
(7)
;
(7)
где σγ1 и σγ2 – среднеквадратические ошибки разброса данных.
Гипотеза о нормальном распределении остатков
принимается, если │![]() 1│<1,5
1│<1,5 ![]()
![]()
![]() и
и ![]()
![]() 2+6 ⁄ (n+1)
2+6 ⁄ (n+1)![]() <1,5
<1,5 ![]()
![]() .
.
Подставив значения εt, t=1,2,…,12 из табл. 1, получим
γ1=0,7654, σγ1=0,55, γ2=-1,0442, σγ2=0,75.
Так как |γ1|<1,5*σγ1 и |γ2+6/(n+1)|<1,5*σγ2, то гипотеза о нормальном характере распределения случайной компоненты εt принимается.
Проверку равенства математического ожидания последовательности εt нулю осуществляют на основе критерия Стьюдента. Значение этого критерия вычисляют по формуле
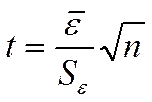 , (8)
, (8)
где
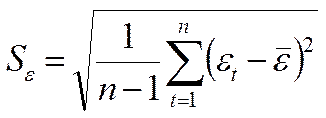 .
.
Для нашего примера ![]() = 0,15/12 = 0,0125,
= 0,15/12 = 0,0125, 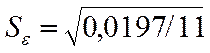 = =0,0423, t = 0,0125
= =0,0423, t = 0,0125![]() /0,0423 = 1,02.
/0,0423 = 1,02.
Табличное значение tα при уровне значимости α=0,05 и числе степеней свободы n-1=11 равно 2,201. Следовательно, гипотеза о равенстве нулю математического ожидания случайной последовательности εt принимается, так как t < tα.
Проверку независимости значений уровней εt выполним по d-критерию Дарбина-Уотсона. Для его реализации требуется вычислить:
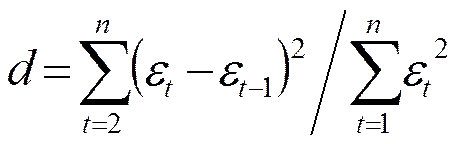 , d΄=4-d. (9)
, d΄=4-d. (9)
Для нашего примера d=2,066, d΄=1,92. Поскольку d>d΄, то гипотеза о независимости значений εt выполняется.
Общий вывод: последовательность остатков εt можно считать случайной компонентой исходного ряда y(t), поскольку удовлетворяет всем четырем условиям.
1. Воспроизведите на экране текст алгоритма по решению системы линейных уравнений методом Гаусса и нарисуйте его блок-схему, изображенную на рисунке.
2. Ознакомьтесь с работой редактора формул. Воспроизведите исходную и конечную (треугольную) системы уравнений, приведенные в разделе «Работа с редактором формул».
3. Введите заголовок «Использование приложений Word и Excel при создании технических текстов».
3.1. Сверните Word путем
нажатия кнопки ![]() в
верхней строке экрана. Вызовите приложение Excel и
сформируйте табл.1, скопируйте её, сверните Excel и, щёлкнув
по полю Word в нижней части экрана, вновь вернитесь в Word.
После введенного заголовка подведите курсор к месту расположения верхнего
левого угла таблицы и щёлкните мышью. Затем подведите курсор к иконке Вставка,
щёлкните по ней, и в результате таблица появится в тексте.
в
верхней строке экрана. Вызовите приложение Excel и
сформируйте табл.1, скопируйте её, сверните Excel и, щёлкнув
по полю Word в нижней части экрана, вновь вернитесь в Word.
После введенного заголовка подведите курсор к месту расположения верхнего
левого угла таблицы и щёлкните мышью. Затем подведите курсор к иконке Вставка,
щёлкните по ней, и в результате таблица появится в тексте.
Далее введите «Результаты проверки модели на адекватность».
3.2. Воспроизведите табл. 2-5 в Excel.
Эти таблицы скопируйте и вставьте их в текст отчета процессора Word. После
каждой таблицы введите фразу о соответствии результатов выдвинутой гипотезе.
Например, данную последовательность остатков ![]() t с доверительной
вероятностью 0,95 можно считать случайной, поскольку Kmax<6 и
t с доверительной
вероятностью 0,95 можно считать случайной, поскольку Kmax<6 и ![]() >3.
>3.
3.3 Сформулируйте общий вывод об адекватности модели.
Таблица 2
Проверка случайности колебаний уровней
|
ε(t) |
|
|
|
сравнение |
|
-0,0436 |
0,0019 |
-0,0001 |
0,0000 |
- |
|
0,0755 |
0,0057 |
0,0004 |
0,0000 |
+ |
|
0,004 |
0,0000 |
0,0000 |
0,0000 |
- |
|
-0,0275 |
0,0008 |
0,0000 |
0,0000 |
- |
|
0,0116 |
0,0001 |
0,0000 |
0,0000 |
- |
|
-0,0481 |
0,0023 |
-0,0001 |
0,0000 |
- |
|
0,024 |
0,0006 |
0,0000 |
0,0000 |
+ |
|
0,0585 |
0,0034 |
0,0002 |
0,0000 |
+ |
|
-0,014 |
0,0002 |
0,0000 |
0,0000 |
- |
|
0,0371 |
0,0014 |
0,0001 |
0,0000 |
+ |
|
0,0424 |
0,0018 |
0,0001 |
0,0000 |
+ |
|
0,0325 |
0,0011 |
0,0000 |
0,0000 |
+ |
|
∑=0,1524 |
∑=0,0192 |
∑=0,0006 |
∑=0,0001 |
Кmax=4 |
|
|
v=6>3 |
Таблица 3
Проверка соответствия остатков нормальному закону распределения
|
Ý1= |
0,7654 |
0,7654 |
< |
0,8321 |
да |
|Ý1|<1,5*δ(Ý1) |
|
Ý2= |
-1,0442 |
0,5826 |
< |
1,1633 |
да |
|Ý2+6/(n+1)|<1,5*δ(Ý2) |
|
δ(Ý1)= |
0,5547 |
0,7654 |
>= |
1,1094 |
нет |
|Ý1|>2*δ(Ý1) |
|
δ(Ý2)= |
0,7755 |
0,5826 |
>= |
1,5511 |
нет |
|Ý2+6/(n+1)|>=2*δ(Ý2) |
Таблица 4
Проверка равенства нулю мат. ожидания
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.