Работа с процессорами Word и Excel при создании технических текстов. Однофакторная модель прогноза уровня спроса на выпускаемую продукцию: Методические указания к лабораторным работам, страница 4

(t -)2	=0,0127	t		tα
0,0032	S=0,0397
0,0039	n=12
0,0001	t=1,109	1,1090	<	2,201
0,0016	=0,05
0,0000	t=2,201
0,0037	t < t
0,0001
0,0021
0,0007
0,0006
0,0009
0,0004
∑=0,0173

                                                                                 Таблица 5

Проверка независимости значений уровней

(ε(t)-ε(t-1))2
0,0142	d=2,0661
0,0051	d’=1,9339
0,0010	∑t2=0,0192
0,0015	d>d΄
0,0036	2,0661	>	1,9339	да
0,0052
0,0012
0,0053
0,0026
0,0000
0,0001
∑=0,0398

    3.4. Для каждого из четырех пунктов проверок введите название проверки, например “Проверка на случайность последовательности ε_t ”. Введите в текст Word соответствующую формулу и результат вычислений, а также вывод по выдвинутой гипотезе.

    3.5. Введите общий вывод об адекватности модели.

Контрольные вопросы  

1.  Элементы стандартного окна Word и их функциональное назначение.

2.  Расскажите о маркировке отдельного слова, строки, абзаца и всей страницы.

3.  Как осуществить ввод текста с учетом заданных полей?

4.  Как удалить символ, несколько символов, абзац, страницу?

5.  Расскажите о выборе размеров шрифта и форматировании.

6.  Состав панели инструментов Рисование.

7.  Назначение элементов панели инструментов Рисование.

8.  Структура редактора формул.

9.  Как вставить графический элемент в документ?

10. Как изменить размеры графического элемента?

11.  Как выделить несколько графических элементов?

12. Как размножить графический элемент?

13.  Как в автофигуру вставить текст?

14.  Как группировать графические элементы?

15.  Как поместить кнопку Редактор формул в панель инструментов?

16.  Работа в редакторе формул.

17.  Как проверить адекватность разработанной модели?

18.  Расскажите об алгоритме проверки случайности остатков.

19.  Как осуществляют проверку о соответствии остатков нормальному закону распределения?

20.  Как осуществляют проверку на равенство нулю математического   ожидания остатков?

Лабораторная работа № 4

Однофакторная модель прогноза уровня спроса

на выпускаемую продукцию

Цель работы. Изучение алгоритма создания однофакторной регрессионной модели и ее применение для прогноза уровня спроса на выпускаемую продукцию на базе табличного процессора Exсel.

Краткие сведения об алгоритме построения модели

Под прогнозированием понимают некоторый процесс, в результате которого получают вероятностные данные о будущем состоянии прогнозируемого объекта. В качестве прогнозируемого объекта в данной лабораторной работе будем рассматривать объем сбыта продукции предприятием. Информация о возможных объемах сбыта продукции в будущем относится к основным вопросам в деятельности любого предприятия, производящего продукцию и занимающегося ее поставкой на потребительский рынок.

Всякий прогноз основан на предшествующей информации и представляет собой временной ряд значений в рассматриваемой задаче объемов сбыта, полученных через одинаковые интервалы времени Dt. Выбор интервала Dt взаимосвязан с длительностью прогноза. Если мы хотим получить прогноз на год, то целесообразно выбрать Dt, равное 0.5 или одному году, если прогноз ориентирован на месяц или два, то, по-видимому, Dt надо взять равным 0.5 или одному месяцу. На качестве прогноза сказывается число членов ряда в наблюдаемый период. Оно должно быть достаточно большим, желательно, больше 10, чтобы выявить тенденцию развития процесса.

Объем сбыта продукции следует рассматривать как случайную величину. Причиной этого является множество факторов, влияющих на него, таких как курс доллара на валютных биржах, изменение цен на аналогичную продукцию конкурентов, изменение тарифов на электроэнергию и транспортные перевозки, качество поставляемого сырья и т.д.

Сущность регрессионного анализа состоит в подборе некоторой модели

Y_m(t) = b₀j₀(t) + b₁j₁(t) + … + b_kj_k(t),                                               (1)

наиболее   соответствующей   набору   экспериментальных   данных,  где       {j_j(t); j=0,1,…,k} -  множество базисных функций.

Основой регрессионного анализа является метод наименьших квадратов, при применении которого требование наилучшего согласования сводится к тому, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой y_m(t) обращалась в минимум, т.е. требуется минимизировать критерий

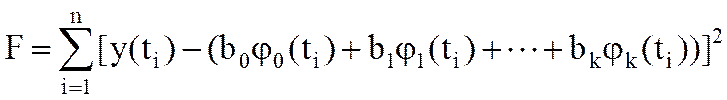
при условии, что число точек измерения n не меньше числа определяемых коэффициентов модели  y(t),  равного  (k+1).