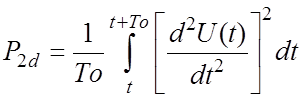Обработка биомедицинских сигналов: Учебное пособие, страница 8

                                                                ,                                    (30)

где P_2d - мощность сигнала второй производной в окне.

При прохождении окном ТР-сегмента мощность сигнала, определенная в соответствии с выражениями (28), (29) или (30), будет иметь минимальное значение Р_МИН, равное дисперсии шума.

Считая, что шум имеет нормальный закон распределения и нулевое математическое ожидание, можно принять значения пороговых уровней U=3σ, где   - среднеквадратическое отклонение. При этом вероятность нахождения отсчетов шума между пороговыми уровнями составит 0.9973. Она и будет определять вероятность правильного выделения опорной точки на ТР-сегменте.

Описанные выше методы  выделения опорной точки в каждом кардиоцикле имеют следующие достоинства:

·  независимость алгоритма выделения опорной точки от вариабельности формы элементов ЭКС, в частности QRS‑комплекса;

·  простой алгоритм и простую техническую реализацию выделения опорной точки в каждом кардиоцикле, в связи с чем повышается эффективность ее выделения;

·  положение опорной точки, предшествующее всем основным элементам ЭКС, позволяет на основании знания морфологии электрокардиосигнала правильно идентифицировать все его элементы;

·  положение опорной точки на участке ЭКС, соответствующем электрической диастоле сердца, позволяет предложить новые подходы к устранению дрейфа изолинии.

4.2. Устранение  дрейфа изолинии

Основной задачей при устранении дрейфа изолинии является выделение из смеси электрокардиосигнала и аддитивной помехи сигнала этой помехи. Известны два пути выделения сигнала изолинии ЭКС, которые могут быть использованы при длительном мониторировании в реальном времени: фильтрационный и интерполяционный.

В первом случае низкочастотные аддитивные помехи устраняются с помощью фильтра верхних частот [21]. Однако в этом случае искажаются параметры ST-сегмента, поскольку частотный спектр дрейфа изолинии, как правило, почти полностью совпадает с частотным спектром ST-сегмента.

Во втором случае на электрокардиосигнале в каждом кардиоцикле выделяются опорные точки, обычно на PQ-сегменте, и через них проводятся аппроксимирующие полиномы, описывающие дрейф изолинии с определенной погрешностью. Наиболее распространенной в настоящее время является сплайн-аппроксимация [19, 22]. Следует отметить, что эта погрешность аппроксимации является методической, то есть принципиально неустранимой. Кроме того, не всегда в электрокардиосигнале присутствует явно выраженный и лежащий на изолинии сегмент PQ, что затрудняет выделение опорных точек. При увеличении частоты изменения сигнала дрейфа изолинии ухудшается точность его восстановления, а при достижении половины частоты следования опорных точек, равной частоте сердечных сокращений (ЧСС), восстановление становится невозможным.

В последнее время появились методы устранения дрейфа изолинии, основанные на применении быстрого вейвлет-преобразования (БВП) [23]. Они используют алгоритмы с прореживанием по частоте, и на каждом последующем этапе преобразованию подвергается низкочастотная составляющая сигнала, полученная на предыдущем этапе.  Применение подобного метода при длительном мониторировании в реальном времени связано с определенными трудностями, обусловленными необходимостью накапливать достаточно большие массивы данных для выполнения БВП и «сшивать» отдельные фрагменты восстановленного сигнала дрейфа изолинии.

Для выделения сигнала дрейфа изолинии можно предложить фильтрационный метод, основанный на использовании фильтра нижних частот (ФНЧ). Сегмент ТР соответствует электрической диастоле сердца. Если на электрокардиосигнал действует низкочастотная аддитивная помеха, проявляющаяся в виде дрейфа изолинии, то на отрезке ЭКС между зубцами Т и Р присутствует только сигнал этой помехи. Таким образом, опорные точки надо выбирать именно на сегменте ТР в каждом кардиоцикле.

Опорные точки, выделяемые на электрокардиосигнале, являются дискретными отсчетами сигнала дрейфа изолинии и представляют собой модулированные по амплитуде прямоугольные импульсы, следующие с частотой сердечных сокращений.

Спектр последовательности таких импульсов содержит в нулевой спектральной зоне составляющие, определяющие исходный непрерывный сигнал [1]. Исходный непрерывный сигнал u(t), в нашем случае это дрейф изолинии, может быть восстановлен, если дискретные отсчеты этого сигнала, т. е. дискретизированный сигнал, пропустить через фильтр нижних частот с полосой частот пропускания, определяемой шириной частотного спектра непрерывного сигнала [24]. На выходе фильтра при этом выделяется полезная составляющая

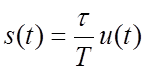,                                                                    (31)

где τ - длительность отсчета,

      Т - период дискретизации,

      u(t) - исходный непрерывный сигнал.

Как видно из выражения (31), выходной сигнал ФНЧ оказывается ослабленным в T/τ раз. Последующим усилением можно довести этот сигнал до уровня исходного непрерывного сигнала. Другим, более удобным для практической реализации, способом является предварительное преобразование дискретных отсчетов сигнала к виду АИМ-2 (расширенные импульсы), в случае которой τ≈T, что не требует последующего дополнительного усиления сигнала дрейфа изолинии.

Преобразование отсчетов в опорных точках в сигналы сложной           формы

Известны импульсные сигналы сложной формы (ИССФ) [25], позволяющие подавить в спектре сигнала любые спектральные зоны. Это свойство ИССФ можно использовать для расширения частотного диапазона аддитивной помехи (дрейфа изолинии), выделяемой из смеси U(t) ЭКС и этой помехи. Сигналы ИССФ представляют собой комбинацию исходного отсчета и нескольких пар элементарных импульсов прямоугольной формы, длительность которых равна длительности τ исходного отсчета помехи, а амплитуда U_i и взаимное положение  τ_i выбираются соответствующим образом из решения системы N уравнений [25]:

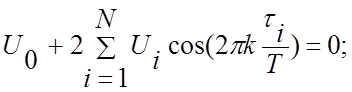
                                                                        (32)

где N – число подавляемых спектральных зон.