Для случая, показанного на рис. 8,а, начальный уровень квантования, то есть уровень с номером 0, совмещается с началом Uмин шкалы сигнала, а последний, то есть уровень с номером N-1, – с концом Uмакс шкалы. При этом шаг квантования определяется выражением
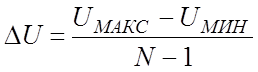. (21)
Для случая на рис. 8,б начальный уровень квантования находится выше начала Uмин шкалы сигнала на 0.5ΔU, а последний уровень – на 0.5ΔU ниже конца Uмакс шкалы. Шаг квантования в этом случае определяется как
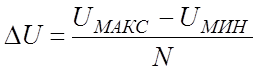. (22)
В случае, представленном на рис. 8,в, начальный уровень квантования совмещается с началом шкалы сигнала, а последний уровень отстоит от конца шкалы на один шаг квантования ΔU. Шаг квантования при этом определяется выражением (22). Данный способ разбиения шкалы сигнала на уровни применяется в современных микросхемах аналого-цифровых преобразователей (АЦП), построенных по принципу поразрядного уравновешивания (например, 1113ПВ1), параллельного (одновременного) преобразования (например, 1107ПВ1).
В описанных вариантах положение начального уровня, а следовательно и конечного, является фиксированным. В некоторых типах аналого-цифровых преобразователей начальный уровень принципиально не может быть привязан к началу шкалы сигнала. Примером такого АЦП являются АЦП последовательного счета и построенные на его основе интегрирующие АЦП. В этих АЦП амплитуда отсчета сигнала U(kTд) преобразуется в пропорциональный временной интервал, который заполняется импульсами с большой частотой повторения. В этом случае реализуется вариант разбиения шкалы сигнала на уровни, показанный на рис. 8,г. Нулевой уровень смещен относительно начала шкалы на некоторую случайную величину dU, 0≤dU<ΔU. При этом последний уровень смещен относительно конца шкалы также на случайную величину ΔU-dU. Шаг квантования в данном случае также определяется выражением (22).
Для отождествления текущего значения отсчета U(kTд) с соответствующим уровнем квантования применяют два способа:
– сигнал U(kTд) отождествляют с ближайшим уровнем квантования;
– сигнал U(kTд) отождествляют с ближайшим меньшим уровнем квантования.
Квантование по уровню неизбежно приводит к погрешности представления сигнала. Эту погрешность называют погрешностью квантования или шумом квантования. Максимальная погрешность квантования Δкв зависит от способа отождествления сигнала с соответствующим уровнем квантования. В первом случае она, очевидно, равна половине шага квантования, Δкв1=0.5ΔU, а во втором случае – шагу квантования, Δкв2=ΔU.
Квантуемый сигнал является случайной величиной. При большом числе уровней квантования, что обычно выполняется на практике, плотность распределения этой случайной величины внутри каждого шага квантования постоянна. Исходя из этого, можно определить среднеквадратическую погрешность σкв квантования сигнала. Для первого способа отождествления сигнала с уровнем квантования
;
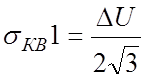(23)
для второго –
.
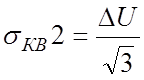(24)
3.3. Соотношение периода дискретизации и шага квантования
При разработке устройств, осуществляющих дискретизацию и квантование биомедицинских сигналов, необходимо выбирать определенное соотношение между частотой дискретизации и разрядностью аналого-цифрового преобразователя (АЦП). Неправильный выбор разрядности АЦП при заданной частоте дискретизации может внести существенную погрешность в определение временных параметров биомедицинского сигнала. Проиллюстрируем это на примере выделения начала зубцов электрокардиосигнала.
При автоматическом определении границ элементов ЭКС используется метод второй производной или, применительно к цифровому представлению сигнала, метод разностей второго порядка [10]. В соответствии с этим методом вычисляют текущие значения разностей второго порядка
,
(25)
где si, si-1, si-2 –значения отсчетов ЭКС в i-й, (i-1)-й, (i-2)-й дискретные моменты времени, разделенные периодом дискретизации.
Для сигнала типа «угол», которым можно аппроксимировать начало зубцов ЭКС, разность второго порядка имеет максимум, совпадающий со значением si отсчета ЭКС в i-й дискретный момент времени. Этот момент времени принимают за начало зубца ЭКС. Значение частоты дискретизации влияет на величину изменения ЭКС между двумя отсчетами. Если это изменение не превышает значения единицы младшего разряда АЦП, то значению d2i будет соответствовать нулевая кодовая комбинация на выходе АЦП. Момент выявления начала зубца ЭКС будет смещаться вправо на один или несколько периодов дискретизации относительно истинного начала зубца до тех пор, пока очередное значение d2i не превысит единицы младшего разряда АЦП. Таким образом, момент начала зубца будет определен с ошибкой, что приведет к ошибочной оценке длительности зубца.
Наиболее высокие требования к числу разрядов АЦП при заданной частоте дискретизации предъявляются при выделении начала Р-зубца ЭКС, поскольку он имеет наименьшую амплитуду и скорость изменения среди всех зубцов электрокардиосигнала с выраженным синусовым ритмом. Внимание к Р-зубцу обусловлено также тем, что начало Р-зубца является началом очередного кардиоцикла и используется в ряде случаев в качестве точки отсчета, по которой осуществляют синхронизацию кардиоциклов при их усреднении, как это имеет место, например, при исследовании поздних потенциалов предсердий и желудочков [11]. Поэтому взаимосвязь числа разрядов АЦП с частотой дискретизации рассмотрим именно на примере Р-зубца. Амплитудно-временными параметрами Р-зубца являются его амплитуда UP и длительность ТР.
Р-зубец можно аппроксимировать полиномом второй степени [10]. В качестве полиномов второй степени, наиболее подходящих для описания Р-зубца, можно использовать степенной полином, а также полиномы Лежандра и Чебышева [8].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.