Общим недостатком данного класса методов является низкая устойчивость к воздействию помех на ЭКС. Для повышения точности оценки параметров ST-сегмента и выделения полезной информации на фоне шумов используются методы усреднения сигнала во временной области в течение нескольких кардиоциклов. Усреднение по времени имеет ряд недостатков. Во-первых, снижается оперативность получения диагностической информации как минимум на интервал времени, за который производится усреднение, что нежелательно при обработке сигнала в реальном времени. Во-вторых, искажения формы ST-сегмента могут присутствовать на кардиограмме в течение незначительного промежутка времени (ишемические эпизоды), поэтому в процессе усреднения информация о наличии патологических комплексов может быть утеряна. В-третьих, из-за наличия вариабельности сердечного ритма длительность ST-сегмента и его положение относительно начала отсчета также не остаются фиксированными величинами, и для точного проведения процедуры усреднения необходимым оказывается нормирование по длительности всех усредняемых комплексов, что требует больших вычислительных затрат и снижает точность.
В интегральных методах [26, 27] для выявлении информативных параметров ST-сегмента используется его спектральное представление в базисе тех или иных ортогональных функций. При этом обеспечиваются снижение воздействия помех на результат обработки ЭКС и более достоверная оценка параметров формы ST-сегмента в пределах одного кардиоцикла.
Рассмотрим особенности выявления диагностической информации об ST-сегменте в его спектральном составе.
В наиболее общем виде элементы кардиоцикла могут быть описаны как суперпозиция варьирующих по амплитуде сигналов-«примитивов. Базовую модель ST-сегмента можно представить в виде суперпозиции трех нормированных сигналов-примитивов: постоянного смещения Uс0, линейно возрастающего сигнала с нулевой ограничиваемой им площадью Uс1 и параболического вогнутого сигнала с вершиной в середине интервала измерения и нулевой площадью под кривой Uс2 (рис. 25).
|
|
|
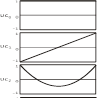
Функция, описывающая сигнал ST-сегмента, примет вид:
up(t)=M0×Uс0(t)+M1×Uс1(t)+M2× Uс2(t),
где M0, M1, M2 - соответствующие масштабирующие коэффициенты.
При обработке реального кардиосигнала областью определения up(t) является интервал времени TST, TST=TJK - TJN (точки окончания и начала ST-сегмента соответственно), который может иметь при расчетах как фиксированную (80 мс), так и изменяющуюся для каждого конкретного кардиоцикла длительность. Для обобщенного представления перейдем к относительному времени θÎ[0, ΘST], ΘST=1.
Для непрерывного сигнала аргумент θ можно выразить следующим образом:
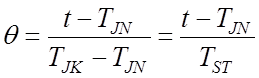 .
.
Рассмотрим спектральное представление ST-сегмента UST(q) в непрерывной форме как наиболее общий случай. При обработке сигнала с использованием средств вычислительной техники (ЭВМ, МК) необходимо дискретное представление ST-сегмента. В дискретном представлении ST-сегмента заменяется его отсчетами в моменты времени ti. Положим i=[0,Im-1], где i – номер временного отсчета ST-сегмента, Im – число отсчетов, принадлежащих ST-сегменту. В этом случае относительное дискретное время
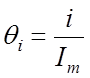 .
.
На интервале относительного времени θ=[0,1] сигналы-примитивы можно представить в виде:
![]()
![]() (42)
(42)
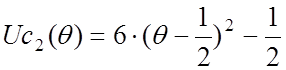 ,
,
соответственно математическое описание ST-сегмента
UST(q)=m0Uc0(q)+m1Uc1(q)+m2Uc2(q), (43)
где m0, m1, m2 - масштабирующие коэффициенты.
При этом значения масштабирующих коэффициентов характеризуют следующие параметры формы: m0 – параметр смещения (ПС), m1 – параметр наклона (ПН) и m2 – параметр выпуклости/вогнутости (ПВ).
В базисе, выбранном для представления ST-сегмента ЭКС, должны присутствовать базисные функции, амплитуда которых определяется наличием и выраженностью в составе сигнала ST-сегмента только одного из «примитивов». Этого нельзя достигнуть при использовании классического аппарата гармонического Фурье–преобразования. При рассмотрении существующих ортогональных базисных функций наиболее подходящим для целей выявления информативных параметров ST-сегмента является базис кусочно-непрерывных функций Уолша.
4.3.2.1. Формирование функций Уолша
Существуют различные способы описания функций Уолша. Рассмотрим способ, основанный на взаимосвязи функций Уолша с функциями Радемахера [3]. Последние, в свою очередь, получаются из синусоидальных функций с помощью соотношения:
rk(J)=sign{sin(2kpJ)}, 0≤J<1, k=1,2,…,
где аргумент J=t/T есть безразмерное время, то есть время, нормированное к произвольному интервалу Т, а целое положительное число k – порядок функции. Символом sign (сигнум-функция) обозначается функция:
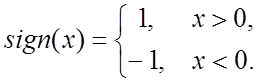
Функции Радемахера, принимающие одно из двух значений - +1 и –1, имеют вид меандра. Все функции Радемахера являются нечетными относительно середины интервала определения и, следовательно, не могут быть использованы для аппроксимации сигналов s(J), четных относительно момента J=1/2. Иными словами, система функций Радемахера является неполной.
Функции Уолша, образующие полную ортонормированную систему, можно сформировать, образуя произведения степеней соответствующих функций Радемахера. Первые восемь функций Уолша были представлены на рис. 7. Сопоставление этих функций с функциями Радемахера позволяет составить соотношения:
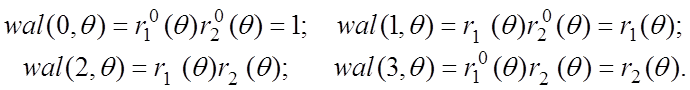
Итак, каждая функция Уолша wal(w,J) за номером w, входящая в систему из N=2n функций, является произведением степеней первых n функций Радемахера. Принцип нахождения этих степеней поясняется в табл. 2 на примере N=8 [1].
Существуют три подхода к порядковой нумерации функций Уолша (по Уолшу, Пэли и Адамару). Упорядочивание функций по Пэли – оптимальный вариант с точки зрения программной и особенно аппаратной реализации формирования базисных функций на основе функций Радемахера. В этом случае номер соответствующей функции Уолша, представленный в двоичном коде, определяет номера перемножаемых функций Радемахера (например, для функции pal(5,q) соответствующий двоичный код – 0101 и pal(5,q)=r40(q)r31(q)r20(q)r11(q) и.т.д.). При дальнейшем рассмотрении будем пользоваться именно нумерацией Пэли как наиболее пригодной для технической реализации преобразования.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.