Обработка биомедицинских сигналов: Учебное пособие, страница 2

отвечающих заданным требованиям. Наиболее типовые требования: определенный диапазон изменения амплитуды сигнала и определенное отношение

 сигнала к шуму (С/Ш). Нормализация сигналов осуществляется с помощью операций усиления и фильтрации.

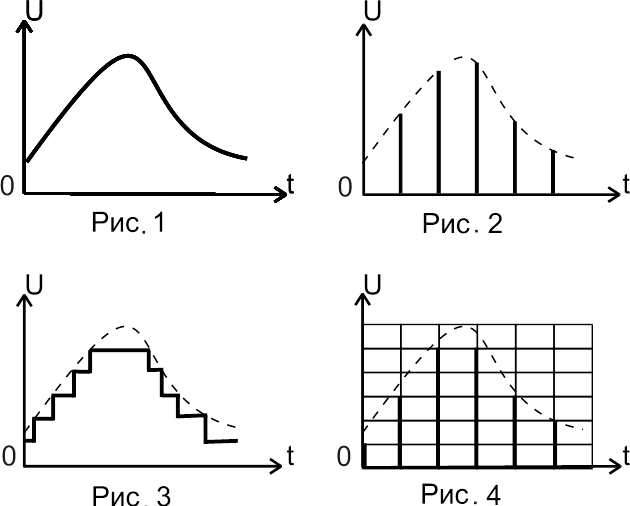
Дискретизация сигналов – это операция преобразования непрерывных во времени и по амплитуде сигналов (рис. 1) в сигналы, непрерывные по апмлитуде и дискретные во времени. При этом непрерывные сигналы представляются в виде отдельных дискретных отсчетов, то есть отсчетов, взятых через определенные отрезки времени (рис. 2). Дискретизация сигналов – первый шаг на пути от датчика сигнала к ЭВМ.

Квантование сигналов или аналого-цифровое преобразование – это операция по замене текущего значения амплитуды  сигнала или его дискретного отсчета соответствующим значением шкалы квантования (рис. 3, рис. 4). Шкала квантования содержит конечное число N уровней  квантования. Операция квантования связана с округлением значения непрерывной величины в соответствии с принятыми правилами (например, отнесение к ближайшему уровню квантования, нижнему или верхнему, или к нижнему уровню квантования). В свою очередь, каждый уровень квантования может быть представлен числом, обозначающим его номер. Если число представлено в виде двоичного кода, то в результате аналого-цифрового преобразования непрерывный сигнал представляется в виде двоичного кода, т. е. становится цифровым.

После обработки биомедицинских сигналов средствами цифровой вычислительной техники содержащаяся в них информация должна быть представлена врачу, исследователю. Человеку же удобнее оперировать не с «0» и «1», а с таблицами, графиками и т. п. Поэтому необходимо сделать обратное преобразование сигнала из цифрового вида в непрерывный, чтобы, например, построить график. Для этого сначала цифровой сигнал с помощью цифроаналогового преобразователя (ЦАП) преобразуется в дискретный (импульсный) сигнал, а затем из дискретного сигнала получают непрерывный сигнал. Преобразование дискретного сигнала в непрерывный осуществляют с помощью операций интерполяции или фильтрации. Фильтрация, как отмечалось выше, используется еще при нормализации сигналов для повышения отношения С/Ш.

Преобразование сигналов из непрерывных в цифровые и обратно связано с изменением спектрального состава сигналов.  Поскольку большинство биомедицинских сигналов имеет выраженную периодичность, для изучения общих вопросов преобразования и обработки таких сигналов рассмотрим спектральное представление периодических сигналов в различных базисах.

2. СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ПЕРИОДИЧЕСКИХ       СИГНАЛОВ

2.1. Обобщенный спектр

Рассмотренные модели сигналов в виде функций времени предназначены в первую очередь для анализа формы сигнала. Реальные сигналы часто имеют достаточно сложную форму (например, сигнал ЭКГ). При исследовании прохождения таких сигналов через радиоэлектронные устройства желательно было бы иметь такое представление сигналов, которое упростило бы это исследование. Для этого сигнал сложной формы удобно представить в виде совокупности каких-то элементарных сигналов.

На практике наибольшее применение нашло представление непрерывного сигнала сложной формы u(t), заданного на интервале (t₁,t₁+T), где Т – период повторения сигнала, в виде линейной комбинации некоторых элементарных функций j_k(t), k=0, 1, 2, …[3]

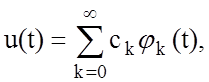                          t₁ £ t £ t₁+T,                                     (1)                                        

где с_k – некоторый безразмерный коэффициент,

       k – порядковый номер функции в системе {j_k(t)}.

Функции j_k(t) называют базисными. При выбранном наборе базисных функций непрерывный сигнал u(t) полностью определяется совокупностью коэффициентов c_k.

Совокупность коэффициентов c_k называют дискретным спектром сигнала, а представление сигнала в виде (1) называют обобщенным спектральным представлением или разложением сигнала по системе базисных функций {j_k(t)}.

Такое представление сигнала удобно для изучения линейных систем. Оно позволяет находить реакцию системы, т. е. сигнал на ее выходе, на любой сложный входной сигнал. Для этого определяют реакцию на каждое элементарное воздействие, полученные результаты умножают на коэффициенты c_k и суммируют, поскольку линейные системы удовлетворяют принципу суперпозиции.

Требования к базисным функциям:

-    для любого сигнала ряд (1) должен сходиться,

-  коэффициенты c_k  должны легко вычисляться,

-  значения коэффициентов c_k не должны зависеть от верхнего предела суммы (1).

Указанным требованиям удовлетворяет так называемая полная, упорядоченная система линейно независимых функций.

Система функций j_k(t), k=0, 1, 2, …, N-1, называется линейно независимой, если равенство

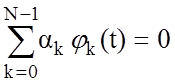                                                                                                            (2) справедливо лишь при a_k=0 для всех k. Это значит, что никакую функцию этой системы нельзя представить в виде линейной комбинации других функций этой же системы.

Упорядоченность означает, что всегда по некоторому признаку можно определить, какая функция является предыдущей, а какая – последующей.

Система линейно независимых функций является полной, если к ней нельзя добавить ни одной новой функции, которая была бы линейно независимой по отношению к функциям рассматриваемой системы.

Если система окажется неполной, то не все сигналы можно представить в виде (1). Например, если мы разложим сигнал по первым 5 гармоникам, то мы не сможем узнать о наличии в сигнале более высокочастотных гармоник.

Неполную систему всегда можно дополнить введением новых функций. В пределе можно получить полную систему.

Коэффициенты ряда (1) просто вычисляются, если в качестве базиса использовать систему ортогональных функций.

В общем случае функции j_k(t), k=0, 1, 2, …, заданные на интервале t₁ £ t £ t₁+T, называют ортогональными на этом интервале, если выполняется условие

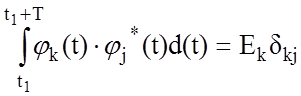                                            ,                                           (3)